(notes edited by Roberto Bigoni)

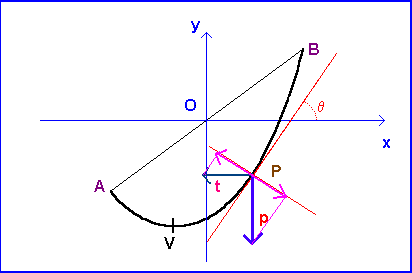
A thin, inextensible, perfectly uniform and flexible rope, suspended between the points A and B, in condition of equilibrium in the constant Earth field g, assumes the shape done by a flat curve said Catenary.
In order to deduce analytically the equation of such curve, we can choose a cartesian orthogonal reference system having origin in the middle point of AB, horizontal axis of abscissas and vertical axis of ordinates.
Let P be a point on arc VP. There are two forces wich act on the punctiform rope element in position P, whose length be dl and mass be dm:
The condition of equilibrium of the point P is due to the fact that the sum of the tangential components of t and p is balanced by the reaction due to inextensibility of the rope, while the components of p and t perpendicular to the tangent balance themselves: therefore their modules are equal.
If we name θ the angle the geometrical tangent to the point P forms with the axis of the abscissas, we shall have
![]()
![]()
Let be y(x) the equation of the curve that describes the disposition of the rope in the chosen system of reference and (x ; y) the cartesian coordinates of the generic P point in such system: tan θ is given by the derivative of the y(x):
![]()
The weight p is due to the weight of the segment VP of the rope.
Let v be the abscissa of the vertex, λ the constant linear density of the rope and g the module of the gravitational acceleration: the module of the weight p is given by
![]()
and therefore
![]()
Deriving both the terms of (5)
![]()
and therefore
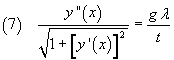
If we introduce the constant k:
![]()
the differential equation admits the solution
![]()
The symbol cosh denotes the hyperbolic cosine.
If we know the coordinates a and b of B (and therefore the coordinates of A, symmetrical of B with respect to the origin O) and the length L of the rope (wich obviously must be greater of AB), we have
![]()
![]()
From (10) we get
![]()
and from (11)
![]()
Dividing term by term the (12) and (13) we have
![]()
and we can express the function (9) in the following form
![]()
From (14) we can also deduce
![]()
Replacing (16) in (12) we obtain
![]()
Given the values of a, b and L , the equation (17) allows to approximate the value of k (different from the banal solution 0).
Since y(a)=b, from (15) we have
![]()
Annulling the derivative of y(x) in (15)
![]()
we can get the abscissa v of vertex V
![]()
The ordinate of V turns out therefore
![]()
The modulus T of the tension, done by the sum of p and t, acting on the point P(x,y) of the rope can be calculated using the Pythagoras's theorem. From (8), (3) e (9) we have
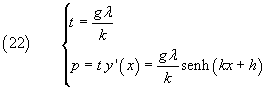
therefore
![]()
![]()
Since the value of g is expressed as 9.81 m/s2, the following Javascript application requires measures in metric units.
last revision: May 2015