Measurement of the heat capacity ratio (γ) of the air
(Clément-Desormes' method)
(notes by Roberto Bigoni)
1. The heat capacity ratio (γ).
The kinetic theory of ideal gases allows us to obtain the Poisson's law for an
adiabatic process:
if A and B represent the thermodynamic states of a gas at the beginning and at the end of an adiabatic process
then
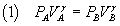
where P and V denote the pressure and the volume and
γ is the ratio between the molar specific heat
at constant pressure cp and the molar specific heat at constant volume cv.
Moreover the kinetic theory of ideal gases allows us to deduce the values of γ
- γ = 5/3 for monoatomic molecules
- γ = 7/5 for diatomic molecules
- γ = 4/3 for polyatomic molecules
To check the validity of this theory we could try to directly measure the values of γ
for real gases made by monoatomic molecules, like helium or neon, or for real gases made by diatomic molecules, like
carbon dioxide, ammonia, methane, in order to see if the results confirm the theoretical predictions.
If we do not have specialized equipment, we can try to measure the γ of the atmospheric air
remembering that it is not a homogeneous gas but a mixture of nitrogen and oxygen with traces of
other gases. Since the air is made mostly of nitrogen and oxygen, the value to be obtained should be close to 1.4.
2. The Clément-Desormes' method.
In order to measure the γ of a gas we must seek to express it as a function of experimentally measurable
quantities. Such quantities can not be cp and cv that are not easily observable, but
other quantities more easily accessible, as are, for example, the pressures.
This path is followed in the method developed by
Clément and Desormes.
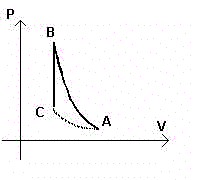
The air inside of a container is subjected to an adiabatic compression that makes it to go from state
A(PA,VA,TA) to the state B(PB,VB,TB).
The temperature TB will be higher than TA.
From the Poisson's law (1) we get
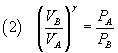
Moreover from the ideal gas law
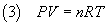
we get
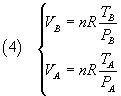
and, dividing these equalities side by side,
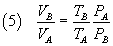
From (5) and (2) we have
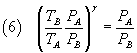
If now an isochoric cooling brings the air from the state B to the state C(PC,VC,TA),
where the temperature returns to TA, from the
Gay-Lussac's law we have
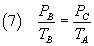
that is
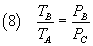
From (6) and (8) we have
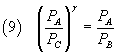
and finally
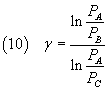
The equation (10) expresses γ as a function of the pressures of the three states to which the gas was taken:
if we are able to measure these pressures we can calculate γ.
To measure these pressures we will use a liquid barometer with liquid density ρ.
If the measures are organized so that PB coincides with the ambient atmospheric pressure P0
(~ 1 Atmosphere), we can express the pressures PA and PC with the
hydrostatic law
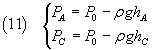
In the equation (10) the numerator can be written as
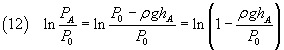
Since if x << 1, ln(1-x) ~ -x, we can approximate this numerator as
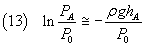
The denominator in the equation (10) can be written as
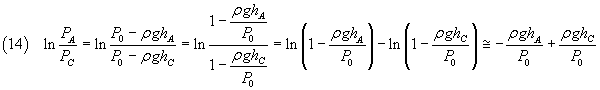
In conclusion, a good measure of γ is given by
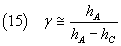
3. Laboratory.
If we want to use the equation (15) for the measurement of the γ of the air
we must force a mass of air, initially in the state A(PA,VA,TA),
to undergo an adiabatic transformation that brings the air to the state B(PO,VB,TB)
and then an isochoric transformation that brings it to the state C(PC,VC,TA)
and we must be able to measure the pressures PA and PC by the heights of a barometric liquid.
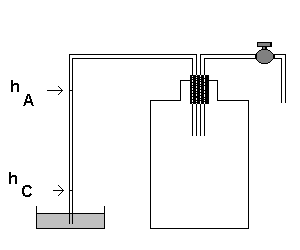
A way to accomplish this experimental situation is as follows.
- We seal a big glass bottle (5 liters or more) with a cap and we insert two pipes in the cap.
A pipe is connected to a liquid barometer, in which the height of the liquid is proportional to the difference
between the external air pressure and the air pressure in the bottle.
The other pipe, provided with a valve to open and close the air flow, is initially connected to a suction pump
(which may be a Venturi tube) and, after,
to the external environment.
Initially, the air in the bottle is at atmospheric pressure PO and at room temperature TA.
- To bring the air in the bottle to the state A, we activate the pump, pulling out a fraction of the air
of the the bottle and producing a depression inside it. The aspiration should continue until the liquid fills
the barometric tube. We must avoid excessively long suction, because the liquid would come in the bottle.
- This aspiration causes an adiabatic expansion of the internal air which is cooled below room temperature.
- At the end of the aspiration, we wait a few seconds and we observe that the liquid level falls from
its peak in the aspiration.
This fact is explained by the flow of heat from the external environment (hot) to the the internal air (cooled)
which continues until thermal equilibrium is established between the interior and exterior of the bottle.
The air inside the bottle is warmed, so its pressure increases, but remains lower than the external one.
- Now the internal air is in the state A in which the temperature coincides with the room temperature TA
and the pressure PA, lower than the external one, can be measured by the height hA of the barometric
liquid. We take this measure.
- To realize the adiabatic transformation AB, we unplug the second tube from the pump and we open the valve.
Since the external pressure is greater than the internal one, there is a flow of air from outside to inside
which produces a rustle in the valve.
The rustling ceases when the internal pressure equals the external one.
As soon as the rustling stops, with precise and decisive move (it is the most delicate phase of the whole operation)
we must close the valve, to isolate the interior from the outside.
During this operation, the air inside the bottle, previously at low pressure PA, is compressed to the
room pressure PO.
If this operation is fast, this compression is adiabatic because the flow of heat from the internal air to the
external is negligible. The adiabatic compression heats the internal air.
- Now the internal air is in the state B
The internal pressure is equal to the external one PO,
but the inner temperature TB is greater than the outer.
- If we wait a few seconds we will observe a rise
the liquid in the barometer.
This is due to the fact that since the internal temperature is greater than the outside, there is flow of heat
from the internal air to the external environment. This flow continues until the re-establishment of thermal
equilibrium between the two environments, that is, until the internal temperature returns equal to TA.
This is the transformation BC that, since the valve is closed, can be considered isochoric,
given the negligible change in internal volume due to the rise of the liquid.
-
When the height of the liquid is stable, the air inside the bottle is in the state C,
with temperature equal to the initial temperature TA and pressure PC, lower than
the atmospheric pressure, corresponding to the height hC of the barometric liquid. We measure hC.
Now we have the measures hA and hC and we can calculate γ from
the equation (15).
Since this measurement technique relies on the ability of the experimenter, the obtained values will be inevitably
subject to random errors: to get a good result and a good evaluation of the uncertainty on it, we will need to replicate
the process many times and then calculate the mean and the standard deviation of the obtained values.
A student's classwork
last revision: October, 2015
![]()

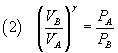
![]()
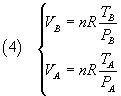
![]()
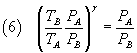
![]()
![]()
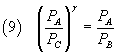
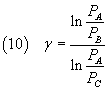
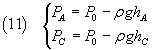
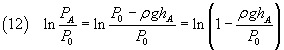
![]()
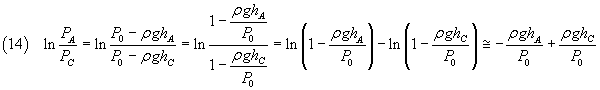
![]()
