The Compton effect

A photon with energy and momentum collides with an electron initially at rest.

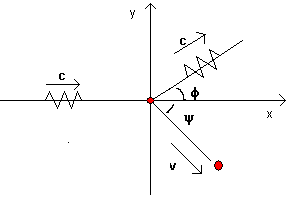
If we represent with m₀ the mass of the electron at rest, with m the mass of the electron after the collision, with φ and ψ the angles of the particles with respect to the direction of the incident photon and and with ν' the frequency of the photon after the collision, from the principle of conservation of momentum we get

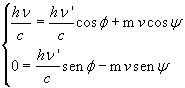
We can eliminate the functions of the angle ψ by carrying it to the left hand side, squaring both sides and adding the equations together:

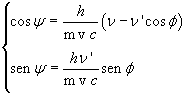
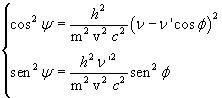
From the principle of conservation of energy, using the relativistic expressions, we get

If we carry m c² to the left hand side and square both sides we have

Now we join together the obtained results

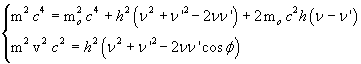
and subtract these equations side by side

The left hand side of this equation is equal to m_o²c⁴: infact

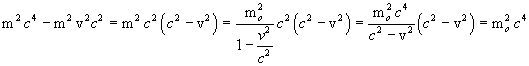
So we get

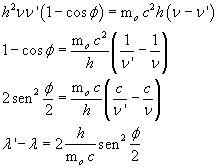
The constant

which is particularly interesting since it results from a combination of three fundamental physical constants, is said Compton wavelength.

Finally, we can write

Scattered photons have wavelengths longer than the incident ones, and these wavelengths depend from the angle at which they are observed.

This effect, observed in 1922 by A. Compton, in the analysis of the scattering of X-rays by a block of paraffin, was in contrast with the classical wave theory so it was one of the most important experimental facts for the development of quantum mechanics.

last revision: October 2015