Rotating systems, centrifugal force, Coriolis force

(notes by R. Bigoni)

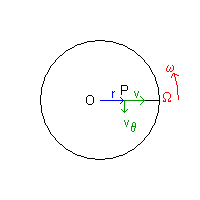
Within an inertial frame of reference I, with origin O, a particle P of mass m, at a given time, moves with constant velocity v toward the observator Ω which is rotating around O with constant angular velocity ω. Viewed by Ω, the velocity of P has not only a radial component v but also a component v_θ perpendicular to the direction OP; this component increases with the distance r = OP.

fig. 1

If we call u_r the radial unit vector OP and u_θ the normal unit vector perpendicular to u_r, viewed by Ω the instantaneous velocity of P is described by the vector

When P lies between P an Ω, viewed by Ω, P is approaching, so the scalar v is negative; the scalar ω must be considered positive when the rotation is counterclockwise, negative otherwise.

Furthermore, viewed by Ω the distance r isn't constant, so also v_Ω isn't constant and the particle P has acceleration given by the derivative with respect to time of v_Ω.

If we assume that the absolute values of v and ω are constant, the chain rule of derivation gives

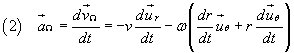
The derivatives of the unit versors u_r e u_θ with respect to time can be obtained in the following way:

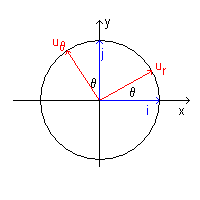
fig. 2

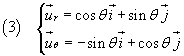
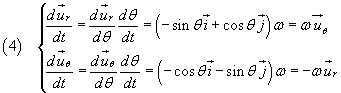
If we now substitute these values in the expression (2), remembering that , we obtain

By the second law of dynamics, the acceleration a_Ω implies the contemporary action of two forces: a radial force

and a tangential force

If we represent the angular velocity as a vector of magnitude ω, perpendicular to the plane of the vectors u_r e u_θ, arising from this plane when the rotation is counterclockwise and entering this plane when the rotation is clockwise, we can write the expression (8) also in the following way:

Forces (7) and (8) aren't ascribable to any real interaction between the particle P and other particles.

Forces like (7) and (8) are said fictitious forces and, since in Ω there are such forces, Ω is a non-inertial frame of reference.

The radial force (7) is said centrifugal force. Within Ω a particle P that within I has constant velocity (also eventually null velocity) seems to be pushed by a force that accelerates the particle outward from the pole O.

The force (8) is said Coriolis force from the name of the french physicist Gaspard Gustave de Coriolis who first understood its nature. Within Ω the particle seems to be acted by a lateral thrust that deflects it from a rectilinear trajectory so it moves along an arc of circle.

If we interpret the fig.1

fig. 1

as the representation of the Earth northern hemisphere viewed by a point above the North Pole O and P as the position of a fluid mass (air or water) moving toward South, we can deduce that the mass P must deflect toward West and perform a clockwise rotation. Similarly a fluid mass moving from the equator toward the North Pole deflects toward East performing a clockwise rotation. Conversely in the southern hemisphere rotations will be counterclockwise. See, for example, the path of the main oceanic streams in NOS Education.

The following Javascript application represents the trajectory of a projectile (in absence of gravity) viewed from a rotating reference frame with origin Ω.
At the beginning, the projectile has position P(x0;y0) and constant velocity with components v_x and v_y. The rotating system, with respect to an inertial system with the same origin, has constant angular velocity ω, positive if the rotation is counterclockwise, negative otherwise.

The following application represents the trajectory of the punctiform mass of an ideal pendulum within a system with origin Ω rotating with angular velocity ω with respect to an inertial system with the same origin.
At the beginning the pendulum, with length l, is in Ω, its velocity has a maximum and is oriented along the abscissa axis.
The trajectory shows the phenomenon known as Foucault pendulum: the plane of the pendulum's swings, which is constant within an inertial reference frame, rotates around the origin Ω.

last reviewed: october 2015