(notes by R. Bigoni)
The conjecture, made by L. De Broglie (1924), that entities such as electrons, with mass and charge (measured by R. Millikan and J. J. Thomson), and arguably with corpuscular properties and behavior, could also have properties and behaviors typical of the waves, such wavelength, interference and diffraction, would probably have remained just an interesting idea, if it had not been supported in a few years by experimental tests such as those made by C. J. Davisson, L. H. Germer, G. Thomson (son of the former).
In particular, Davisson and Germer, by experiments similar to those made by W. H. Bragg and his son, W. L. Bragg (1913) on X-rays, were able to highlight that an electron beam, reflected from the planes of a crystal lattice, produces diffraction patterns.

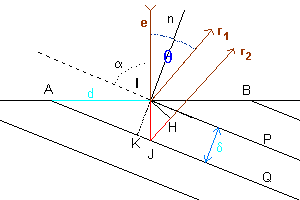
With reference to the figure, e represents an electron beam, which hits the surface of a crystalline solid, represented by the line AB, at the point I, forming the angle α with the crystal plane represented by the line IP.
A portion of the beam is reflected from the plan IP in the direction r1, forming with the normal n to this plane an angle of reflection equal to the angle of incidence. The angle θ between the incident beam and the reflected one is
![]()
Another portion of the incident beam hits at the point J the crystal plane JQ, parallel to the plane IP and with distance δ from this one, and is reflected in the direction r2, parallel to r1.
If the reflected beams r1 and r2 are formed by waves, they overlap and interfere with each other. If the difference between the optical paths is equal to an integer number of wavelengths, the interference is constructive. If instead the difference between the optical paths is equal to an odd number of half wave-lengths, the interference is destructive.
The difference between the optical paths of the two emerging beams is given by the sum of the measures of the segments IJ and JH (in red in the figure).
In the the right triangle IKJ we have
![]()
In the the right triangle IJH we have
![]()
The sum of the two measures is
![]()
Moreover, if we represent by d the measure of the segment AI,
![]()
![]()
Therefore, the interference is constructive when
![]()
and destructive when
![]()
Davisson and Germer observed that, when a crystal is irradiated with electrons accelerated to the energy K, then with momentum
![]()
and, according to the De Broglie's equation, with wavelength
![]()
the intensity of the reflected beam has maxima and minima depending on the value of the angle θ.
These maxima and minima, which can be explained as due to constructive or destructive interference, provided a formidable support to the hypothesis that electrons and other subatomic particles are provided with wave-like properties.
Example
The surface of a sample of nickel is irradiated with electrons accelerated by a potential of 54 volts. The parameter d, measured by the X-ray diffraction, has value 2.15·10-10 m.
The wavelength of the electrons is
![]()
We will observe a maximum for
![]()
last revision: October 2015