(notes by R. Bigoni)
A small magnetic needle shows that near the wires carrying electric current there is a field of magnetic induction B (Oersted effect).
This field has vectorial nature because in every point it has a magnitude and an oriented direction. If the wire is rectilinear and infinitely long, its direction is perpendicular to the plane containing the wire and whatever straight line from the point to the wire. The orientation is such that if the observer on the wire sees the current moving away, the induction is clockwise and vice versa.
Obviously, an infinitely long wire is an asymptotic condition which can be physically approximated by taking a long wire and exploring the field near it away from its ends.
Measuring in vacuum the magnitude of the field of magnetic induction, usually represented by B, varying the distance from the wire, one can find that it is directly proportional to the intensity of the current i and inversely proportional to the distance from the wire d (Biot-Savart's law).
(1.1)
The proportionality constant μo in the expression of B is called vacuum magnetic permeability; in metric units its value is
(1.2)
In order to calculate the magnitude of B in whatever point P near whatever wire, one can conjecture that every infinitesimal electric charge dq, in every infinitesimal wire segment dl, gives an infinitesimal contribution dB proportional to dq, to its velocity v and to the sine of the angle θ formed by the velocity and the straight line joining the charge and the point P; furthermore, like in Newton's and Coulomb's laws, this contribution is inversely proportional to the square of the distance from dq to P.
(1.3)
The vector dB is
(1.4)
In (1.3) one can let
and
, so
the (1.3) can be rewritten as
(1.5)
The validity of the (1.5) can be tested by deducing from it the experimental Biot-Savart's law.
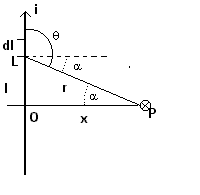
In the figure, the current flows upward in a vertical infinitely long wire. The infinitesimal wire segment dl makes the angle θ with the vector r from L to P. r forms the angle α with the perpendicular PO from P to the wire. Let x be the measure of the segment PO and l the measure of the segment OL
With these substitutions the (1.5) becomes
and, because x = r cos α,
(1.6)
The whole magnitude of B in P will be
(1.7)
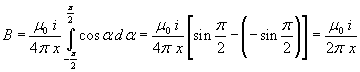
This is the same as the (1.1). So we can think the (1.5) is a good formula.
The (1.5) allows to go beyond the experimental result expressed by the Biot-Savart's law and to deduce the magnitude of B near more complex electrical circuits.
The simplest case consists in finding B in a point P on the axis of a ring carrying a constant current i.
In such points the direction of B coincides with the axis itself. In fact, if we consider two diametrically opposed infinitesimal segments of the ring, it is evident that their contributions dB to B in P have equal magnitude. The angles formed by these dB with the axis are geometrically equal. Their components perpendicular to the axis are opposite, so their sum is null. Their components parallel to the axis are equal and have the same direction, so their sum is the double of a single component. The orientation of the sum is from the plane of the ring to the point P if looking the ring from the point one sees the current circulating counterclockwise and vice versa.
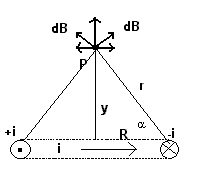
With reference to the figure, the contribution dB of every infinitesimal element dl of the ring, from the (1.5), is
but only the component parallel to the axis is effective
(2.1)
The resulting magnitude of B in P can be obtained by integrating the (2.1) on the whole length 2πR of the ring
(2.2)
In order to have the magnitude of B in terms of the distance y from the point P to the plane of the ring, one can express r as the hypotenuse of the right triangle with catheti R and y:
(2.3)
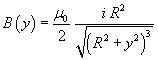
From (2.3) one can immediately deduce the magnitude of B in the center of the ring:
(2.4)
It is also interesting the value of the magnitude of B in a point of the axis
at a distance
from the ring plane:
(2.5)
In order to create in a point P a magnetic field quite strong and easily controllable
one can connect two coaxial coils, having an equal number N of rings with the same
radius R, carrying the same current i, distant R the one from the other.
This device, called Helmholtz coils, is such that in its central point, at the
distance
from both of them, the field BH is axial and has magnitude
(3.1)
For example, if the coils have radius R=10cm, have 500 rings in which there is
a current i=10A, in vacuum we obtain
This field is about 400 times stronger than that of the Earth.
The field BH is approximatively constant between the two coils.
The electrons injected with velocity v perpendicular to the field BH
created by the Helmholtz coils undergo a Lorentz force having magnitude
This force that is perpendicular to the velocity acts as a centripetal force and the electrons, while they are in the magnetic field, cover a circumference arc with radius R given by the equality
(4.1)
in which the centripetal force equates the Lorentz force.
From the (4.1) one can deduce the charge-mass ratio of the electron (its specific charge)
(4.2)
The speed of the electrons of a beam can be calculated by the knowledge of the accelerating potential in the electron gun which generates the beam. The electrons energy is eV and is equal to their kinetic energy
(4.3)
From the (4.3) we have
and from the (4.1)
. By joining
together these equations we have
(4.4)
Finally, by putting this result into the (4.2), we obtain
(4.5)
The properties in the second term of the (4.5) can be experimentally measured and therefore they allow the measurement of the specific charge of the electron. By joining this value with the value of the electric charge e of the electron obtained by Millikan, it is possible to evaluate the the rest mass of the electron.
In order to find the measure of the radius of curvature of the electronic beam R, one can show the beam on a table drawn with squares. If the origin O of a cartesian frame of reference is placed at the beginning of the beam, to calculate the radius it is sufficient to get the coordinates of any other point P of the beam.
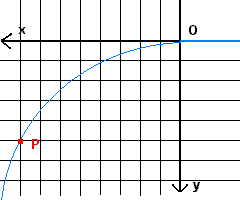
In fact, the equation of the circumference with center in C(0;R) and radius R is
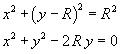
If the point P belongs to the circumference, we have
and finally
(4.6)
For example, with reference to the figure,
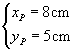
Therefore, from the (4.6), the radius of curvature of the beam is
last revision 20/10/2015