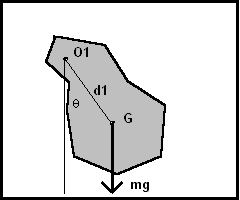
(notes by Roberto Bigoni)
A rigid body of mass m, suspended from a fixed point O1 in the field of the constant terrestrial gravity acceleration g is in equilibrium when the moment of the weight force P=mg, applied to its center of gravity G, with respect to the constraint O1, is null, that is, when O1 and G are on the same vertical line. The equilibrium is stable when G lies below O1.

If the body is moved away from the stable equilibrium position by an angle θ, the intensity of the moment of force is
![]()
where d1 is the distance between O1 and G. The negative sign indicates that if the angle θ is positive (that i counterclockwise) the moment is negative and causes a clockwise rotation and vice versa.
If θ is very small, its sine is well approximated by the angle itself and we can write
![]()
The moment of a force is given by the derivative of the angular momentum. If we denote by I1 the moment of inertia of the body with respect to the axis of rotation passing through O1 and perpendicular to the plane of rotation, we have
![]()
Equating the right hand sides in (1.2) and (1.3) we have
![]()
The equation (1.4) shows that the second derivative of the angle with respect to time is proportional to the opposite of angle itself. From this we can deduce that, for small initial displacements, the motion of the pendulum is of harmonic type, with angular frequency ω1 given by
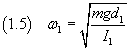
If now we overthrow the body and hang it to a point O2, aligned with O1 and G and distant d2 from G, and let it swing, we obtain the angular frequency ω2
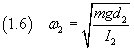
We remember that, by definition, the angular frequency ω of a harmonic motion is inversely proportional to the period T
![]()
The Kater's reversible pendulum is made of a rigid metal bar on which are inserted two massive discs M1 and M2 that can scroll along the bar and be fixed in different positions in order to change the position of center of gravity of the pendulum. Moreover, the pendulum is provided with wedge-shaped knives O1 and O2, so that we can hang it on a vertical rigid support and swing it around O1 and O2.
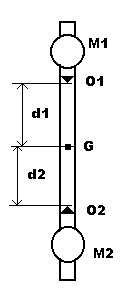
By appropriately placing the masses M1 and M2, we can obtain that the period T1 of the oscillations of the pendulum when it is standing at O1 is equal to the period T2 of the oscillations we obtain by reversing the pendulum and hanging it on O2.
In this case also the angular frequencies are equal and therefore, by equating their expressions (1.5) and (1.6), we obtain
![]()
and then
![]()
We can apply the parallel axis theorem
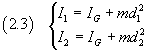
and rewrite the equation (2.2) as
![]()
Solving the equation (2.4) in the unknown IG, we obtain
![]()
and substituting this expression of IG within the first one of the equations (2.3)
![]()
and substituting this expression of I1 within the equation (1.5)
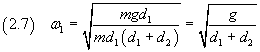
Finally, if we denote by d the distance d1+d2 between the two knives, and we recall the equation (1.7), we obtain
![]()
We have implicitly assumed that the gravitational mass that appears in the expression of the weight and the inertial mass appearing in the expression of the moment of inertia coincide: this issue would merit to be better developed.
The equation (2.8) coincides with that valid for the simple pendulum, when the length l of the simple pendulum is replaced by the distance d between the knives of the Kater's pendulum and the period T of the simple pendulum is replaced by the period T for which the Kater's pendulum is reversible, ie the common value of the periods of the oscillations on the two knives O1 e O2.
If we can measure d and T, the equation (2.8) allows us to get the measure of g.
![]()
![]()
Because of the difference between the equatorial radius and polar radius of the Earth and the centrifugal force due to the diurnal rotation, g, at sea level, decreases from the poles to the equator as a function of latitude.
From the equation (2.10) the relative uncertainty on the measure of g is
![]()
In order to obtain a good measure, d and T must be large enough and the absolute uncertainties on the measures of d and T must be minimized. If you want to be able to appreciate the third decimal place of g, the order of magnitude of their relative uncertainties must of 10-3.
If d is approximately one meter, Δd must be one millimeter or less; If T is about one second, ΔT should be one millisecond or less. If you have a manual chronometer to one hundredth of a second, you can measure the duration of 10 periods and then divide by 10 the measure and its uncertainty.
The measurement of T is the more laborious for the practical difficulty of identifying the positions of the masses M1 and M2 such that, by inverting the pendulum, the period remains unchanged.
For this purpose, you could initially fix the position of M1 and move from time to time the position of M2, starting from the lower end of the bar and gradually bringing it closer to M1, for example by 10 cm at a time. For each position of M2, you can record the measures of T1 and T2, so as to compile a table like the following
| M2 (cm) | T1 (sec) | T2 (sec) |
|---|---|---|
| 10 | ||
| 20 | ||
| 30 | ||
| 40 | ||
| 50 | ||
| 60 | ||
| 70 | ||
| 80 | ||
| 90 |
Given the points whose abscissas are the values of the positions of M2 and whose ordinates are the values of T1 and T2, you can draw a graph, tracing the curves through these two sets of points. The intersection of the two curves allows you to evaluate the value of d and T to be used in the equations (2.10) and (3.1).
last revision: May 2025