notes by Roberto Bigoni
(In the following text, vector quantities are represented by letters in bold; in the numbered equations vector quantities are topped with an arrow, the scalar (or dot) product is denoted by · and the vector cross product is indicated by ×.)

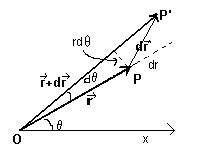
The position of a point P in a plane can be represented by choosing a polar reference system with pole at O and polar axis OX and by matching the point P with a vector r with magnitude equal to the measure of the segment OP and polar angle θ given by the measure of the oriented angle XOP.
If, with an infinitesimal change in position, the point P moves to P', the new position is represented by the vector r', ie the vector sum r+dr.
dr represents an infinitesimal displacement, which in turn can be expressed as the sum of two infinitesimal vectors, one of which is radial, that is directed as PO and with magnitude dr, and the other one is tangential, that is perpendicular to OP, with magnitude r dθ.
I we represent with ur the radial unit vector and with uθ the tangential unit vector, we can write
![]()
Since the velocity vector is the derivative with respect to time of the position vector, we obtain
![]()
The first term in the right hand side of (1.2) is the radial component of velocity or, more briefly, the radial velocity; the second term is the tangential component of velocity or, more briefly, the tangential velocity.
With a convention introduced by Newton, we show the first derivative of a quantity with respect to time by superimposing a dot to the symbol of the quantity. Adopting this notation we can rewrite the equation (1.2) in the following way
![]()
Moreover, often the derivative of the polar angle θ with respect to time, said angular velocity,
is represented by the symbol ω.
Then we can also write the following version of of (1.2)
![]()
The square of the velocity vector is
![]()
By definition the acceleration vector is given by the derivative of the velocity vector with respect to time:
![]()
To obtain the acceleration we derive the equation (1.2.2)
![]()
To derive the radial and the tangential unit vector, we can represent them in a cartesian system of coordinates.
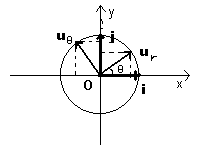
If we call i and j the units vectors of the cartesian axes, we have
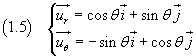
The derivatives of the equations (1.5) with respect to θ are
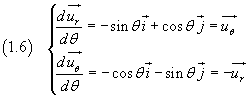
then
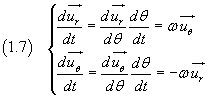
Now, from the equations (1.7) and (1.4), we get
![]()
and finally
![]()
If the magnitude of the position r is constant, the motion is a circular motion centered on the pole O.
In this case, the radial velocity is zero so the velocity coincides with the tangential velocity.
Therefore, in the case of a circular motion, we obtain
![]()
If in a circular motion ω is constant, the motion is called uniform circular motion.
In a uniform circular motion, if T is the period, ie the duration of a full rotation, we have
![]()
and the expression of the acceleration, from the equation (1.9), is simply
![]()
that is, the acceleration has only the radial component which is constant and directed from the point to the pole.
In this case the acceleration is said to be centripetal.
The work of a force f which causes an infinitesimal displacement dr of its point of application, by definition, is
![]()
From the second law of motion
![]()
and from the equation (2.1) we have
![]()
Moreover, differentiating the square of speed, we obtain
![]()
Then the right hand side of the equation (2.3) becomes
![]()
where
![]()
K is called kinetic energy.
So, from the equation (2.1), we obtain
![]()
that is
![]()
If a body (which we assume to be point-like) with mass m moves with velocity v, its momentum p is given by p=mv.
If the body is in the position r with respect to the pole O, its angular momentum with respect to the pole O is
![]()
If we derive both the sides of the equation (3.1) with respect to time we get
![]()
The first vector product in the right hand side is zero, since the derivative of the position vector is the velocity vector that is parallel to the momentum.
The derivative of the momentum with respect to time, from the second law of motion
![]()
is the force acting on the body. Therefore, in general
![]()
In the equation (3.3) the vector τ, given by the vector product of position and force,
is called moment of the force or torque.
The equation (1.3) can be seen as an extension of the second law of motion to the angular quantities:
f matches τ, p matches l and
τ is the derivative with respect to time of l as f is the derivative with respect to
time of p.
If f is a central force, ie parallel to r, its moment is zero; so also the derivative of the angular momentum with respect to time is zero, that is the angular momentum of a central force is constant.
If a vector is constant, its direction and its magnitude are constant.
The direction of angular momentum, which is the vector product of r and p,
is perpendicular to the plane of r and p:
this means that r and p, during movement of the body, are always on the same plane;
therefore the trajectory is a plane curve that is covered by the body always with the same sense of rotation.
As a first approximation, ie neglecting the forces due to the presence of other planets, according to the theory of Newton, the force of universal gravitation acting on a single planet is a central force directed from the planet toward the Sun,
![]()
therefore, according to this law, the planets follow orbits that are described by planar curves and are free of retrograde motion.
The magnitude of l is rp sinδ where δ is the angle between the vectors r and p, so p sinδ is the tangential component of the momentum, that is the product of the mass by the tangential velocity. The tangential velocity is ωr, then
![]()
ω is the derivative with respect to time of the polar angle θ, then
![]()
r2dθ can be geometrically interpreted as twice the area dA swept by the position vector
![]()
Therefore, ultimately
![]()
Since the right hand side is constant, also the left hand side, said areal velocity, is constant.
This is the second of Kepler's laws, obtained by him by accurately recording the positions of the planets visible to the naked eye over time, and traditionally formulated in the following way:
A line joining a planet and the Sun sweeps out equal areas during equal intervals of time.
This is the same as saying that the areal velocity is constant; as we have seen, this is an astronomical result, of the fact that, if a body is subjected to a central force, its angular momentum is constant.
By definition, the work of a force is given by the scalar product of the force and the displacement vector.
To calculate the work of the force of gravitation related to an infinitesimal displacement dr we need to perform the scalar product of force (3.4) for the infinitesimal displacement (1.1)
![]()
The right hand side in (4.1) is the opposite of the exact differential of the function
![]()
If we represent this function, said gravitational potential energy, with U, the equation (4.1) can be written as
![]()
By the theorem of live forces
![]()
If we subtract the equation (4.3) from (4.4) we obtain
![]()
So the total energy E, sum of potential and kinetic energy, of a body with mass m located in the gravitational field generated by a body with mass M (assumed at rest in the pole O) is constant over time
![]()
For this reason we say that the gravitational field is a conservative field.
From the equation (4.6) we obtain the square of the velocity
![]()
Using the expression (1.2.3) of the square of the velocity, we have
![]()
and after
![]()
From the equation (3.5) we have
![]()
so we can rewrite the equation (5.3) as
![]()
![]()
Using again the equation (3.5)
![]()
we have
![]()
Now we divide the equation (5.6) by the equation (5.5) and separate the variables
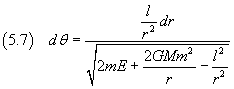
To simplify the differential expression of the right hand side, it is useful to let
![]()
and
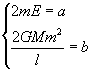
With these substitutions the equation (5.7) can be rewritten as
![]()
The integration of the differential at right hand side is facilitated by writing the radicand as a difference of squares
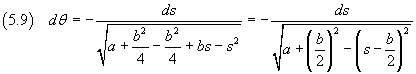
Now we integrate
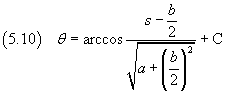
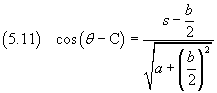
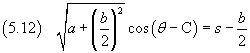
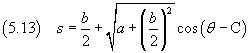
Remembering the value of s:
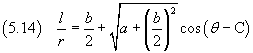
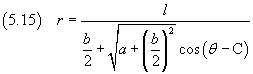
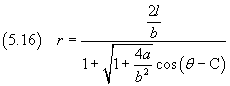
If we impose that r has its maximum when θ = 0, we get C = π and then
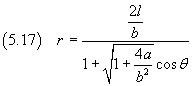
The equation (5.17) is the polar equation of a conic with semilatus rectum p and eccentricity e given by
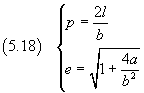
Remembering the values of a and b we have
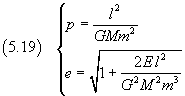
In particular, by examining the expression of the eccentricity, we can see that
This result is more general than that stated by Kepler's first law: 'The orbit of every planet is an ellipse with the Sun at one of the two foci', because it provides that the heavenly bodies in the gravitational field of the Sun or another star, can also move along parabolic or hyperbolic orbits.
For simplicity sake we will consider only circular orbits.
If the orbit is a circumference, the eccentricity is 0, so, from the equation (5.19)
![]()
Moreover the gravitational force is a centripetal force that can be expressed by the equation (1.12)
![]()
We can simplify:
![]()
![]()
The velocity can be expressed using the equation (1.10)
![]()
The total energy E=U+K is
![]()
From the equations (6.1) and (6.6) we obtain
![]()
![]()
Recovering l from the equation (3.5)
![]()
![]()
Recovering ω from equation (1.11)
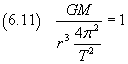
![]()
The equation (6.12) expresses Kepler's third law: The square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit.
In order to calculate the position of a planet as a function of time, referring to the diagram below, we can proceed as follows.
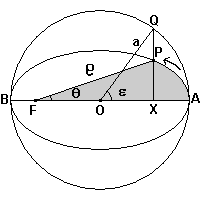
In the Cartesian system with origin O and axes coincident with the axes of the ellipse, the distance FO has measure ae and the abscissa x is common to the points P and Q.
In this system, the equation of the circle is
![]() then the ordinate yQ of the point Q of the circle is
then the ordinate yQ of the point Q of the circle is
![]() .
.
In the same system the equation of the ellipse is
![]() , then the ordinate yP
of the point P of the ellipse is
, then the ordinate yP
of the point P of the ellipse is
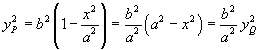
so the lengths of the segments PX and QX are such that
![]() .
.
This implies that:
![]()
the area of the ellipse is b/a of the area of the circle
![]()
the area of the region of ellipse with vertices XAP area is b/a of the area of the region of circle with vertices XAQ.
![]()
To calculate the area of the region XAQ we make the difference between the area of the circular sector OAQ and that of the triangle OXQ. We get
![]()
and then
![]()
We get the area of the whole elliptical sector FAP (with a dark background in the figure) by adding the area of the triangle FXP and the area of the region XAP
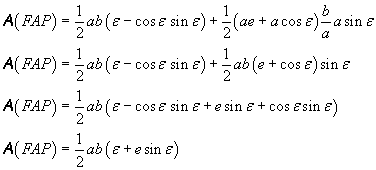
This is the area 'swept' by the radius vector FP in time t. For the second Kepler's law, the ratio between this area and the time t is constant; in particular it is equal to the ratio between the whole area of the ellipse and the period T of revolution:
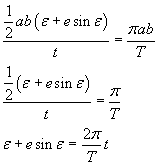
If we represent the mean angular velocity with ω,
![]() ,
we finally get
,
we finally get
![]()
This equation, known as Kepler's equation, given the orbital period T of a planet (or satellite) and the eccentricity of its orbit, allows to compute the eccentric anomaly ε.
Having computed the eccentric anomaly ε, we can derive the true anomaly, for example, in the following way:
From the relation between sin θ e sin ε
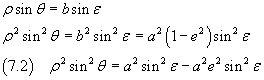
Moreover
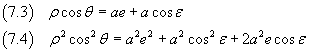
If we sum the equations (7.2) an (7.4) we have
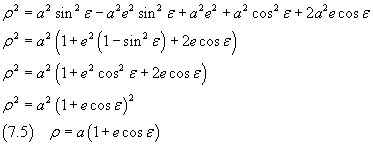
Now we consider together the equations (7.3) and (7.5)
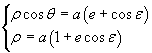
and divide side by side
![]()
Remembering the half-angle formulae
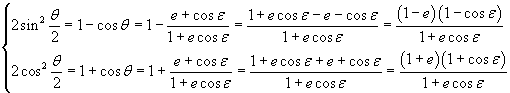
we can get
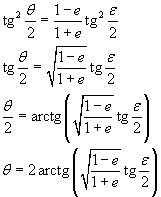
If θ is negative, we can increase it by 2π
After obtaining θ, we can calculate the radius ρ using the polar equation of the ellipse.
last revision: April 2017