To test the effectiveness of the Schrödinger equation in a very simple and well analyzed case, now we will work backward, to show that this equation allows to deduce energy levels and wave functions for a particle confined in a well bounded by insurmountable vertical barriers. 'Insumountable' means that beyond the barriers the potential is infinite. We suppose that between the barriers the potential is null and that the velocity of the particle is perpendicular to the barriers, so the problem is one-dimensional.
We have to resolve the equation (7.9), that is
![]()
Since the problem is one-dimensional and the particle states are stationary, we can use a simplified version of (7.9):
![]()
A function such that its second derivative with respect to its argument coincides with its opposite is the sine. So we may let
![]()
Its derivatives are
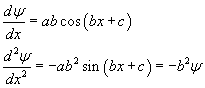
The second derivative coincides with (8.1) if
![]()
Moreover the function (8.2) must be 0 when x=0 or x=L.
ψ(0) = 0 implies c=0.
ψ(L) = 0 implies
![]()
and therefore
![]()
These are the energy eigenvalues.
From (8.3) and (8.4) we have
![]()
and, using this value of b in (8.2),
![]()
To define the parameter a we use the normalization condition (5.13)
![]()
![]()
from which we have
![]()
Ultimately, eigenfunctions are
![]()