9. Particle in a one-dimensional finite depth square well.

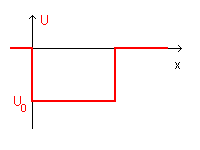
Now we will consider a one-dimensional field in which the potential V is everywhere 0 except on the interval [0;L] where the potential energy of a particle is negative with constant value U₀ < 0. Intervals like this are said one-dimensional potential wells with depth U₀.

In Classical Mechanics a particle with positions 0<x<L and total energy lesser than 0 but greater than U₀ can not escape from the well because outside it its kinetic energy K = -0 would be negative.

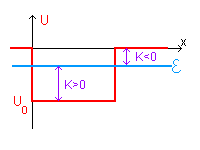
The Quantum Mechanics approach is the following:

• if 0<x<L the wave function must be a solution of the equation (the subscript _I stands for 'Internal')

  

• if x<0 or x>L the wave function must be a solution of the equation (the subscript _E stands for 'External')

  

Since the wave function must be continuous and differentiable in the entire field, for x=0 or x= L the two solutions and their derivatives must have the same values.

Moreover, since the Quantum Mechanics approach must asymptotically converge to Classical Mechanics, x→±∞ ⇒ ψ → 0.

• With a method similar to that taken in the previous section 8, we assume for the equation (9.1) a solution and, in the same way we obtain

  

  But in this case, we cannot assume the boundary conditions ψ(0)=0 e ψ(L)=0, because the walls of the pit have finite altitude. So, for now, we have

  

• Solutions of (9.2) can not be something like , because the second derivative implies a negative value to the the square of b. If we otherwise assume solutions like ψ(x) = a e^{b x}, differentiating twice with respect to x we have

  

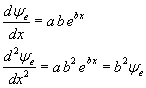
  and the comparison with (9.2) gives

  

  This equality is acceptable because, by hypothesis, is negative. Therefore outside the well the function may have the form

  

• Since the wave function must be zero for x→±∞, we assume (the subscript _EL stands for 'External Left' and the subscript _ER stands for 'External Right' )

  • for x<0:
  • for x>L:

For x=0 the two solutions and their derivatives must be equal. So

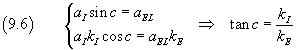
The same happens for x=L. So

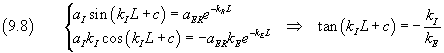
From (9.6) and (9.8) we have

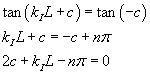
Finally, using the values of c and k_I from (9.3) and (9.7), we have

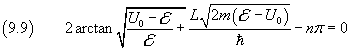
By solving this equation with respect to for each value of n we can obtain the energy levels inside the well. There is no analytical way to calculate thise solutions, but they can be approximated at will with a numerical method beginning from n=1 and raising it while negative solutions are found.

Here there is a Javascript function that calculates energy levels of an electron in a one-dimensional well, given its width, measured in nanometers, and its depth measured in volts.

JS uses the simple bisection algorithm. The code is in the HTML source of this page.