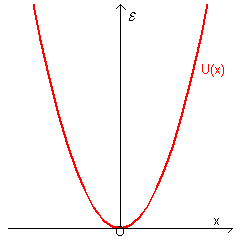
From (2.13), the graph of the potential energy of a one-dimensional harmonic oscillator with respect to the distance x from its equilibrium position, is a parabola with vertex at the origin O and up concave.
A particle with finite total energy
that moves with harmonic motion is contained into a infinitely deep potential well so the probability to find it
at infinite distance is zero.
In this case the Schrödinger equation is
and, taking U(x) from (2.13),
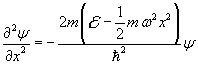
This last equation can be simplified by the variable subtitution
from which
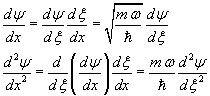
so, from (10.2) we have
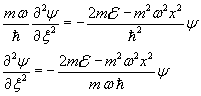
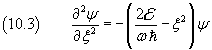
We can have a more simple notation of (10.2) if we let
so
The solution of this equation must approach 0 as ξ approaches positive or negative infinity: we may express it as
where φ(ξ) is a function to be determined later.
By substituting this expression and its second derivative with respect to ξ in (10.5) we have
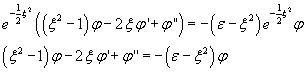
Now we assume that the solution φ of (10.7) may be expressed by a series expansion
and therefore
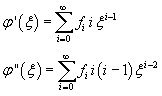
By substituting these values in (10.7) we have
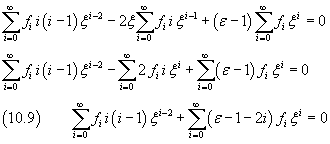
Since φ does not have singularities, we cannot consider negative exponents, so
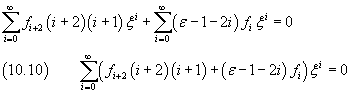
The sum (10.10) is identically zero if and only if all its coefficients are zero
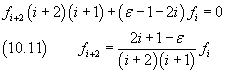
The equation (10.11) establishes a recursive relationship between the coefficients of the series expansion(10.8) of φ(ξ)
Moreover, since φ(ξ) must be finite for any ξ, there must be an index n of the expansion such that the not-zero n-th term would produce the (n+2)-th term equal to 0 an so all the following terms with indexes (n+4), (n+6) and so on. Therefore, from (10.11) we obtain
that is, from (10.4)
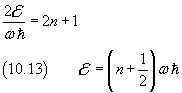
If we use the Planck constant instead of the Dirac constant we have
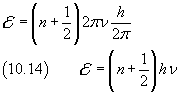
The equation (10.14) represents a fundamental result in the history of Physics of the twentieth century, because it provides a theoretical justification to the Planck conjecture and improves it: harmonic oscillators, contrary to that provided by Classical Mechanics, may not have any energy, but their energy is quantized. The minimum value of the energy of a quantum oscillator id given by (10.14) with n=0. All other possible energy values differ from that for multiples of hν. So a harmonic oscillator can emit or absorb energy only if it exchanges with the outside blocks of energy multiples of hν.