If a particle P with mass m is attracted by a body S at the origin O with a force inversely proportional to the square of its distance x (x > 0) from S, its potential energy is expressed by a function having form
where C is a positive proportionality constant depending on P, S and on medium between them. In this case the potential well has an outline like the following
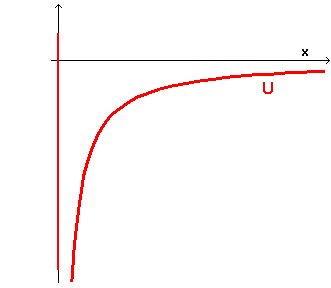
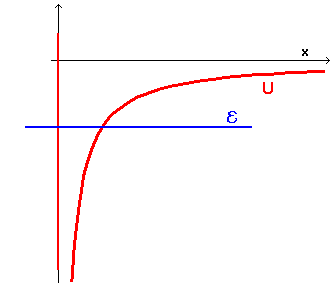
If the total energy
of the particle is negative, the graph
of energy is like this
The Schrödinger equation in this case is
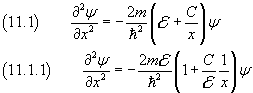
If we let
we have
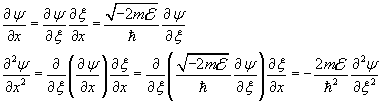
and after, from (11.1.1),
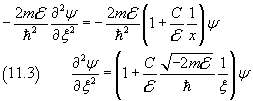
To simplify the notation we let
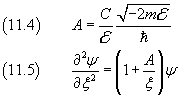
x→∞ ⇒ ψ→0 , so we may assume
where φ is a function to determine later, with a singularity for ξ=0 but finite for every other ξ.
By differentiating twice the ψ(x) in (11.6) with respect to ξ we have
and this expression of the second derivative in (11.5) gives
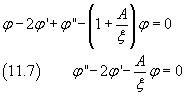
Now, like in the previous section, we assume that
and therefore
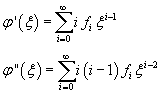
By using these values in (11.7) we obtain
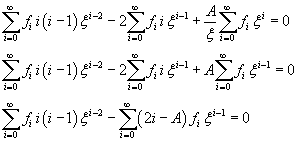
Since φ is not defined for x=0, we do not consider the terms of the expansion with negative exponents of ξ
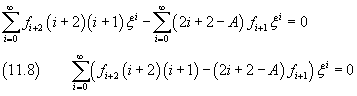
The sum in (11.8) is zero only if all the coefficients of the powers of ξ are zero:
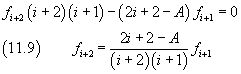
Like in the previous section, we have obtained a recursive relationship between the coefficients of the series expansion. Furthermore, the expansion reduces to a polynomial, and therefore is finite for every ξ, if a not zero coefficient is followed by a coefficient equal to zero. Let k be the index of the last not zero coefficient. From (11.9) we obtain
that is A must be a not zero even natural number (in (11.10) n represents a natural number ≥ 1).
By recovering the definition of A from (11.4), from (11.10) we obtain
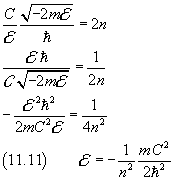
Once more we reach the conclusion that the energy of a particle can have only discrete, quantized, values. The minimum value is
If the particle is an electron in the field of a proton, we have
and, from (11.1),
The equation (11.13) coincides with that obtained by N. Bohr to explain the hydrogen spectrum, under the hypothesis that the electron has circular orbits such that its angular momentum is an integer multiple of the reduced Planck constant
In fact, if r is the orbital radius and v the electron speed, from (11.14)
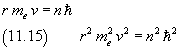
Coulomb's force is a centripetal force
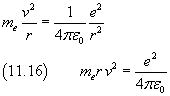
By dividing the equation (11.16) by the equation (11.15) we obtain
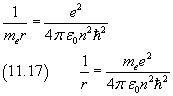
The total energy of an electron with circular orbit in the field of a proton is
Finally, from (11.17) and (11.18) we obtain (11.13)
In conclusion, the Schrödinger equation provides a general theoretical foundation to explain results previously obtained on the basis of ad hoc hypotheses, like these of Bohr, assumed to justify specific experimental data.