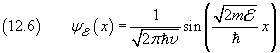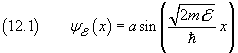12. Wave function of a free particle.

The description of the quantum mechanical state of a free particle may be derived from the results got in section 8 as asymptotic case with L (distance between walls) approaching the infinity. Obviously now we can't apply the same boundary conditions as there but, like there, we can assume

.

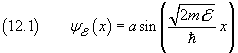Instead to the energy, we can refer the wave function to the momentum

The wave amplitude is now expressed as α because it depends on the normalization procedure of the function.

In order to normalize the function ψ_p we cannot simply make equal to 1 the integral of the square of the equation (12.2) from -∞ to +∞, because this integral, which is essentially a sum of an infinite number of positive quantities, diverges. Since ψ_p is a continuous function of a continuous variable p, we will integrate the square of the integral intermediate value of ψ_p on the interval [p₀ , p₀+Δp],

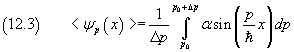
The integration gives

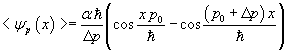
Considering progressive and regressive waves the normalization condition results

The integration gives

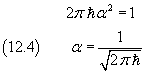
Therefore the equation (12.2) can be more fully written as

To write the wave equation in terms of energy, we change the differential in (12.3)

so that

This gives

.

In conclusion, the wave equation of a free particle with energy is