Let m be the mass of a particle P and f be an elastic force, that is a force proportional to the displacement Δr of P from the point O, where f is equal to 0, and with direction opposite to this displacement
![]()
In this case, the equation of the motion of P can be expressed by a function with the following form
![]()
A particle moving in this way is called a harmonic oscillator.
To obtain the (2.2) it is convenient to select a reference system with origin in O and the x-axis coincident with the direction of the displacement. In this system the equation (2.1) becomes
![]()
If we apply the second law of dynamics, we obtain
![]()
and we can rewrite the equation (2.3) as
![]()
Moreover, i we let
![]()
we obtain
![]()
The solution of the differential equation (2.7) must be a function x(t) such that its second derivative with respect to t is the opposite of the same function multiplied by ω2. A function with this property is
![]()
In fact
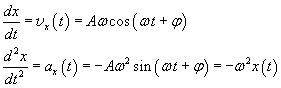
In the equation (2.8) the parameter A, which represents the magnitude of the maximum value of the displacement x(t), is called amplitude.
The parameter φ, called phase shift, is the argument of the sine at time t=0.
By requiring that x(0)=0 and vx(0)=Aω, the phase shift is zero and the equation (2.8) can be written more simply
![]()
To understand the physical meaning of the parameter ω, we represent with T the time elapsed between two successive maxima of the function x(t) in the equation (2.9). This function has its maxima when sin ωt=1, that is when
![]()
then
![]()
![]()
The quantity T is called period and can also be defined as the duration of a complete oscillation. The reciprocal of T, called frequency, is usually indicated with ν (greek n) and represents the number of oscillations per unit time.
![]()
The quantity ω, said angular frequency, is proportional to the frequency and thus substantially provides the same physical information.
Using the equation (2.6), we can rewrite the equation (2.3) as
![]()
When the force f moves its point of application of a quantity dx, it does the work
![]()
and the variation of potential energy corresponding to the displacement x is
![]()
Ultimately, the total energy of the harmonic oscillator is
![]()
The energy of the harmonic oscillator is constant and depends on the mass and the on the squares of the amplitude and of the angular frequency.