Refraction.

When a wave crosses the boundary surface between two media in which it propagates at different speeds, the energy can flow out completely from the first medium to the second one only if the two media have the same impedance. Otherwise, only part of the power can be transmitted in the second medium and the remainder is reflected.

If we represent by Z₁ and Z₂ the impedances of the media, by I_i the intensity of the incident wave, by I_r the intensity of the reflected wave and by I_t the intensity of the transmitted wave, from the principle of conservation of mechanical energy we have

Furthermore, we assume that the amplitude at the points of the surface is continuous

So we have

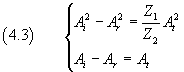
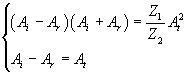
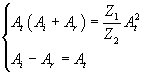
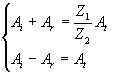
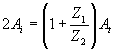
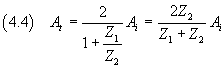
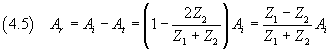
The equations (4.4) e (4.5) show that:

• if the impedances are equal, the transmitted amplitude coincides with the amplitude of the incident amplitude and the reflected amplitude is zero;
• if Z₁ is much greater than Z₂, the transmitted amplitude tends to 0 and the reflected amplitude tends to coincide with the incident amplitude;
• if Z₁ is much smaller than Z₂, the transmitted amplitude tends to twice the incident amplitude and the reflected amplitude tends to coincide with the incident amplitude.

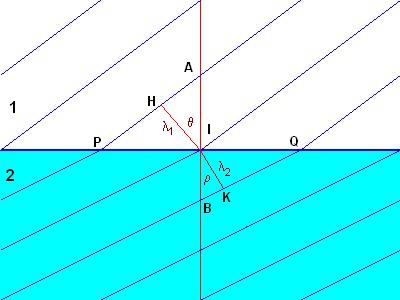
In the figure, the black parallel lines in the half-plane 1 (white background) represent the wavefronts of a plane wave with velocity v₁ and wavelength λ₁ which crosses the surface of separation between the medium 1 and the medium 2 (blue background) in which the wavefronts are represented by blue parallel lines, the velocity v₂ has magnitude less than that of v₁ and the wavelength λ₂ is less than λ₁.
The line AB is perpendicular to the surface of separation and the segments HI and IK are perpendicular to the wavefronts.

Since the wavefronts are continuous, the segments are PI and IQ are equal. If we denote the angle HIA by θ and the angle BIK by ρ, we have

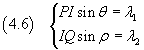
Dividing side by side the equations (4.6) we have

Sinceλ=vT and the period T is the same in the two media

The ratio between the speeds is a specific constant of the pair of two media; it is called the refractive index of the first medium with respect to the second one and is usually written n_1,2.

The equation (4.9) is known as Snell's law or Descartes' law.