
If a beam of polarized monochromatic light is projected against an opaque diaphragm, on which there is a small circular hole, we can observe on a screen placed beyond the diaphragm the bright image of the hole. But the shape of this image does not coincide, as we might expect based on everyday experience, with that of the hole. Instead it is a bright spot surrounded by rings of decreasing brightness separated by dark rings.

This is a diffraction pattern and can be explained only by attributing a wave nature to light.
If, to simplify the analysis, we assume that on the diaphragm, instead of a hole, there is a thin straight slit perpendicular to the plane of polarization, assumed linear and constant, of a plane wave and moreover we accept the Huygens' principle, that is that every point of the slit behaves as a primary source of circular waves that propagate beyond the diaphragm with equal speed and reach a single point P on the screen at different times and then out of phase with each other, then, if the difference between the distances of the point P from the two points A and C of the slit, A located on one edge and B in the center, is equal to half wavelength, at the point P, the elementary waves interfere negatively, and produce a dark area. The point P thus marks the position of the first dark fringe and therefore OP is half of the central bright fringe.
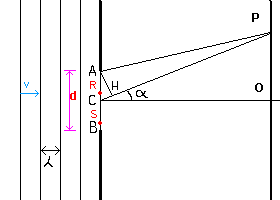
If O is the point of the screen on the geometrical axis CO of the segment AB, and we denote by d the length of the segment AB and by α the angle OCP and assume that the distance CO is infinite with respect to d, we have
![]()
The same relationship holds for any other pair of points R and S, R in the segment AC and S in the segment CB, such that RS = AC, then the rays RP and SP interfere as AP and CP.
P represents the position of a bright fringe if
![]()
and the position of a dark fringe if
![]()
To deduce the trend of the intensity of illumination, we may consider the slit AB as composed of infinitely many pairs of slits R and S, both of infinitesimal width dx and symmetrical with respect to C, from which both have the same distance x.
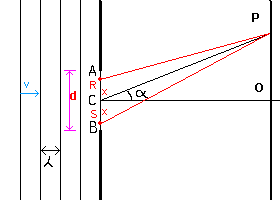
If we denote by Amax the maximum amplitude, which is obtained by symmetry in the point O, the contribution of each pair to its maximum is
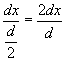
and from the equation (5.4) we have
![]()
The total amplitude at P is obtained by summing all the contributions dA from 0 to d/2:
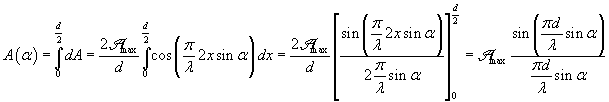
and consequently the intensity is
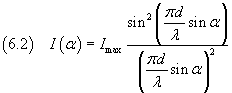
Example: the intensity pattern for λ=d/3
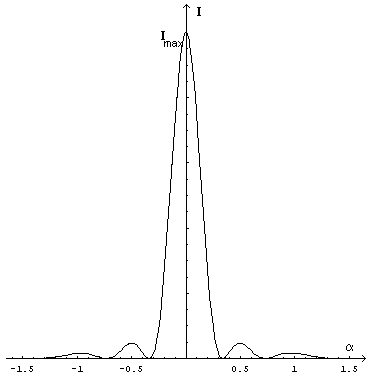
animation