Standing waves.

If a point of the medium that supports wave is forced to be immobile, its energy is always 0 and then the energy can not flow through it:this point is a barrier that prevents the wave to pass him.

To simplify the understanding of the phenomenon we can consider one-dimensional waves as, for example, those that propagate on the strings of musical instruments. In these strings, which in this case are the media of the propagation of energy, the extremes are immovable, fixed to the instrument, and therefore they can not vibrate like other points of the string. Their energy is constantly equal to 0 and then the energy can not flow through them.

As happens to a particle that hits a rigid wall with velocity perpendicular to the wall itself, when the wave reaches an extreme, it reverses its speed and propagates in the direction opposite to that from which it comes until it hits reaches the other extreme, by which it is reflected once again an so on.

Progressive and regressive waves mutually interfere and produce, as a result, a wave forced to have nodes at the ends of the string. This condition implies that the length of the medium must contain exactly an integer number of half wavelengths.

If L is the length of the medium and λ the wavelength

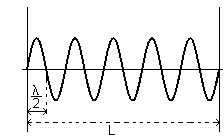
This id a standing or stationary wave. When a medium holds a standing wave, all its points behave as harmonic oscillators with the same angular frequency ω but with amplitudes that vary depending on their distance from the extremes.

In a reference system in which the abscissa of an extreme is 0 and that of the other is L, with an appropriate choice of the initial instant, the state of the medium at time t is described by the equation

in which the amplitude C sin kx must be 0 when x is a multiple of a half wavelength, in particular when x is equal to a half wavelength:

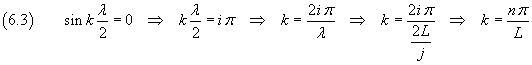
So we have

The equation (5.4) is the equation of the n-th stationary wave function on a one-dimensional medium with length L and having nodes on either end.

The constant C depends on the total energy distributed in the medium.

If μ is the linear density of the one-dimensional medium

recalling equation (3.9), the energy of an infinitesimal mass dm which oscillates with angular frequency ω and amplitude A is

In the equation (6.4) the amplitude is , so

The sum of the energies of all the infinitesimal mass dm, extended to the whole medium, is the total energy residing on the medium

From the equations (6.5) and (6.6) we have

and then

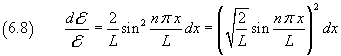
The equation (6.8) shows that the fraction of the total energy between x and x+dx is proportional to the square of

that is the energy density at the position x is proportional to the square of ψ_n.

The square of ψ_n represents the distribution function of the energy density along the x axis.

Since the equation (6.9) is independent of μ, it is true not only for material waves, but for any wave.

Then, if we let

in the equation (6.4), we have

This is the equation of the n-th wave equation that can exist in one-dimensional medium with length L, normalized so that the square of the amplitude represents the relative density of energy.

The same wave function (6.11) can be more concisely written

where

If many waves overlap in the same medium, all supposed to have nodes on the ends of the medium itself, the interference between these waves, called harmonics, produces rather complicated wave configurations. This is what happens, for example, in the vibrant parts of musical instruments in which the emitted note depends on the fundamental harmonic and the timbre depends on the mixing of different harmonics, due to the shape and the stuff of the sound box.

If we interpret the energy density as the probability density of the presence of energy in a given position, the equation (6.13) obviously represents the certainty of the fact that all the energy of the system is situated in the interval [0 ; L].

if we consider, within this range, the positions x₁ and x₂, the integral

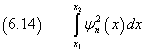
represents the probability that there is energy within the interval Δx = [x₁ ; x₂].

If we consider a system formed by a large number of interfering harmonics, we observe that this probability decreases to 0 except in a narrow range in which the totality of the energy appears concentrated. If the number of harmonics tends to infinity, the size of this range tends to 0.

This interval is not static, but moves with constant speed, bouncing off the barriers just like a particle would.

We can then vice versa conjecture that a particle, with kinetic energy and momentum p perpendicular to the walls, can be described by a system of infinite harmonics.

By accepting this conjecture, if the number of harmonics is not infinite, the magnitude of Δx is > 0; that is there is an uncertainty on the position of the particle, the greater the lesser is the number of the harmonics.