(from Note Didattiche)
In the Cartesian plane xOy, if a2+b2+4c>0, an equation with form
![]()
represents a circumference with center C
![]()
and radius
![]()
Since in the equation (1) there are three parameter (a, b, c), three independent conditions are sufficient to completely determine the equation of the circumference.
In particular, given three non collinear points P, Q and R:
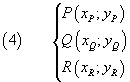
the equation of the circumference through the three points can be determined by imposing that the coordinates of the three points satisfy the equation (1), that is, by solving the system
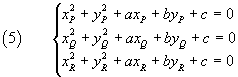
It is possible to solve the problem in other ways, for example, by calculating the equations of the axes of the segments PQ and QR and the coordinates α and β of the point C where the axes intersect. C is the center of the circumference. The distance of C from one of the three points is the radius ρ. The equation of the circumference is given by
![]()
The following Javascript application automates the solution of the problem. If the coordinates of the points are rational (ie do not contain the decimal point but can contain a slash), also the parameters a, b and c are expressed by rational numbers.
The application calculates equation, center and radius produces the graph of the circumeference.
The application works only if your browser allows Javascript and popup windows.
last revision: September 2018