Notes by R. Bigoni
(from Didactic hints)
In the Cartesian plane xOy an equation like
![]()
may represent a conic.
Since the coefficients A, B, C, D, E, F in (1) are defined up to a proportionality factor, in order to calculate them will be sufficient five independent conditions, that can be the coordinates of five points P, Q, R, S, T, such that
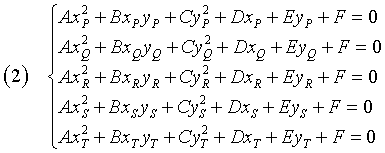
To obtain determined coefficients we can complete the system with an arbitrary normalization condition that imposes that the equation is of 2nd degree: for example A + B + C = 1.
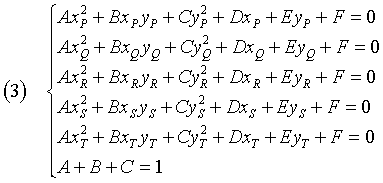
The following Javascript application provides the solution of the problem.
When all the coordinates of the points are rational (ie they do not contain the decimal separating point and may contain the fractional bar),
the coefficients A, B, C, D, E, F are also expressed by exact rational numbers.
The coordinates can also be expressed in fixed or floating point or as expressions (eg 1.2+1/4) or as function values (eg Sqrt[2], Sin[1]).
In this case the coefficients are approximated by real numbers with the decimal part rounded to the number of digits in the decimals field.
last revision: September 2018