notes by R. Bigoni
(from Didactic hints)
An equation of second degree in x e y
![]()
where A, B, C, D, E, F are real coefficients defined up to a proportionality constant k (k≠0) and A, B, C are not all equal to zero, may represent a conic.
Let d: ax+by+c=0 be the equation of its directrix, with a and b not both null, e its directrix and Φ(xΦ,yΦ) its focus.
We therefore have the following equations
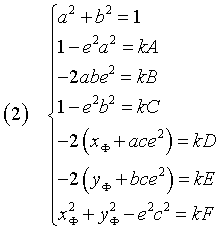
By subtracting side by side the fourth equation of (2) from the second one we have
![]()
From (3), A=C ⇒ (e = 0) ∨ (a2 = b2).
From the third one of (2), B = 0 ⇒ (e = 0) ∨ ((a = 0) ∧ (b = 1)) ∨ ((a = 1) ∧ (b = 0)).
Then ((A=C) ∧ (B = 0)) ⇒ (e = 0), that is, the conic is a circumference and the directrix does not exist.
In this case the (1) becomes
![]()
With the method of completing the squares we have
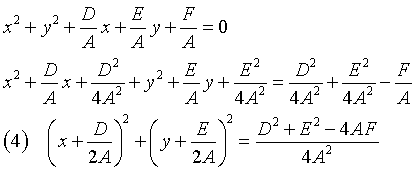
The (4) is the equation of a circumference with center Ω and radius ρ
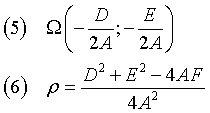
The circumference is real only if ρ is positive.
If (A ≠ C) ∨ (B ≠ 0), the conic is not a circumference and has positive eccentricity. Let Δ be
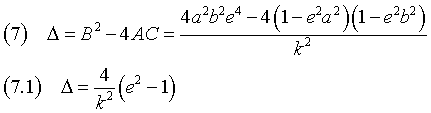
Therefore:
With A ≠ C, joining the (3) with the first one of the (2)
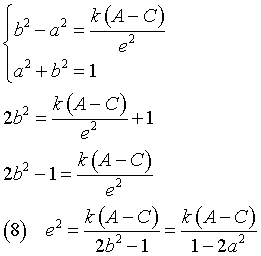
If the eccentricity is positive, from the third of the (2), B = 0 ⇒ (((a = 0) ∧ (b ≠ 0)) ∨ ((a ≠ 0) ∧ (b = 0))
Then, if B = 0, the conics has directrix parallel to one of the Cartesian axes.
From (8)
(B = 0) ∧ (A-C > 0) ⇒ (a = 0) ∧ (b ≠ 0)
(B = 0) ∧ (A-C < 0) ⇒ (a ≠ 0) ∧ (b = 0)
3.1 Parabolas
If (B = 0) ∧ ((A = 0) ∨ (C = 0)), from the equation (7), the equation (1) is the equation of a parabola with eccentricity e = 1. We have the following particular cases.
(A = 0) ∧ (B = 0): the (1) becomes
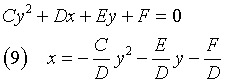
The (9) is the equation of a parabola with directrix d parallel to the y axis, vertex V and focus Φ.
To simplify the notation, let α, β γ be
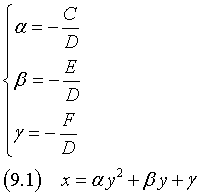
We have
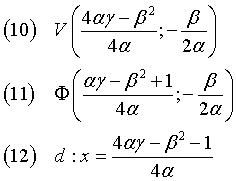
(B = 0) ∧ (C = 0): the (1) becomes
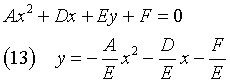
The equation (13) is the equation of a parabola with directrix d parallel to the x axis, vertex V and focus Φ.
To simplify the notation, let α, β γ be
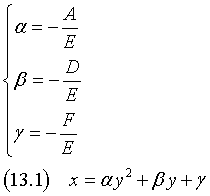
We have
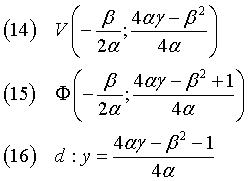
If (B = 0) ∧ (A ≠ 0) ∧ (C ≠ 0), if (A < 0), it is convenient to multiply by -1 both sides of the equation.
3.2 Ellipses
If (B = 0) ∧ (AC > 0), from the (7) the (1) is the equation of an ellipse. We have the following particular cases.
(B = 0) ∧ (A > 0) ∧ (C > 0) ∧ (A < C) ⇒ (a ≠ 0) ∧ (b = 0): the (1) becomes
![]()
The conic is an ellipse with directrices parallel to the y axis and a focal axis parallel to the x axis.
By completing the squares
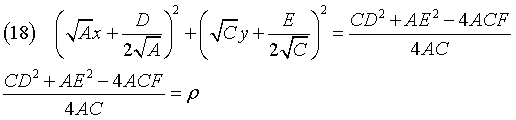
If ρ is not positive, the ellipse is not real. Otherwise it has center Ω and semiaxes α and β
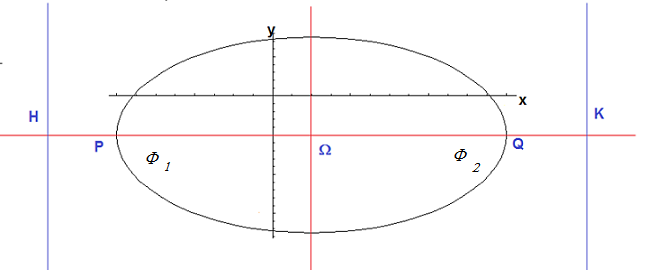
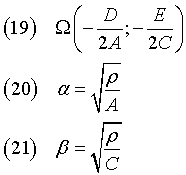
The distance φ of the foci from the center Ω and the eccentricity e are
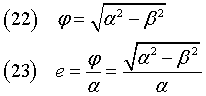
The coordinates of the foci Φ1 and Φ2 are
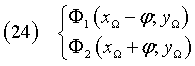
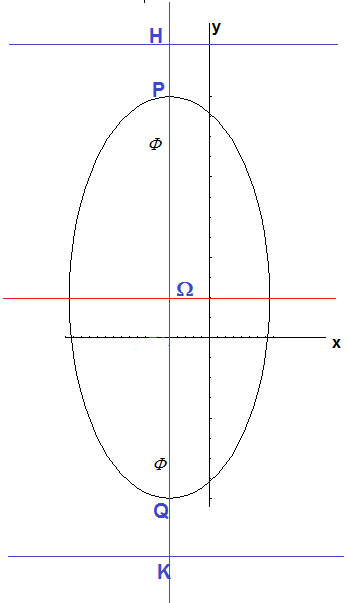
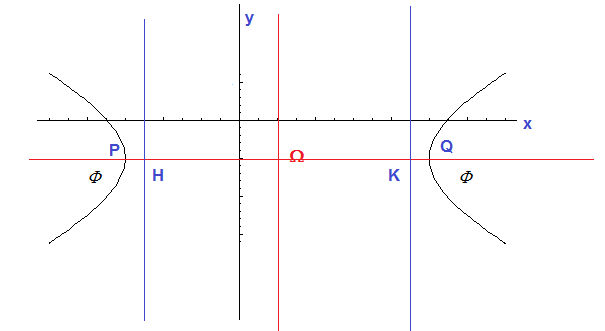
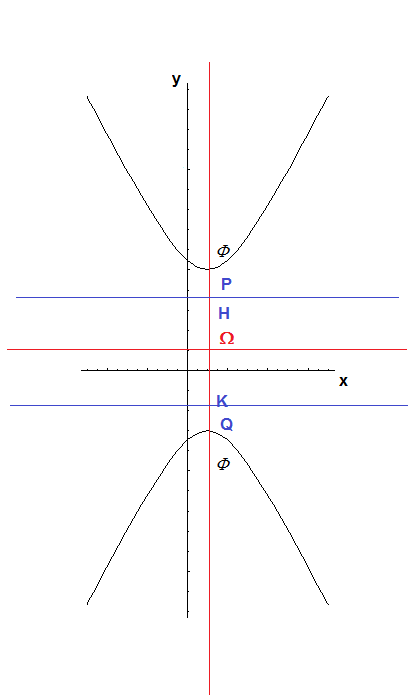
Let P and Q be the points of intersection of the conic with the focal axis (xP < xQ) and H and K the points of intersection of the focal axis with the directrices (xH < xK); we have
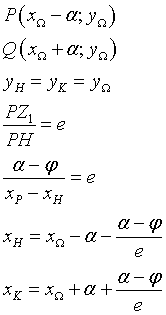
Therefore the equations of the directrices are
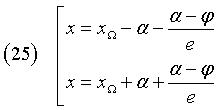
(B = 0) ∧ (A > 0) ∧ (C > 0) ∧ (A > C) ⇒ (a = 0) ∧ (b ≠ 0): the (1), as in the previous case, becomes
![]()
The conic is an ellipse with directrices parallel to the x axis and focal axis parallel to the y axis.
By completing the squares
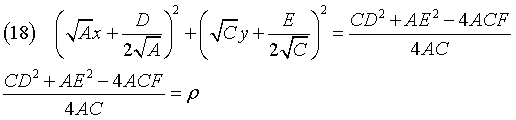
If ρ is not positive, the ellipse is not real. Otherwise it has center Ω and semiaxes α and β
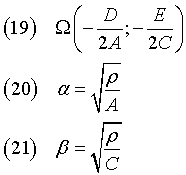
The distance φ of the foci from the center Ω and the eccentricity e are
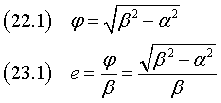
The coordinates of the foci Φ1 and Φ2 are
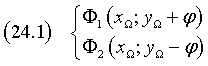
Let P and Q be the points of intersection of the conic with the focal axis (yP > yQ) and H and K the points of intersection of the focal axis with the directrices (yH > yK); we have
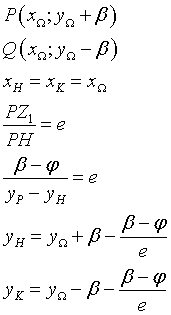
Therefore the equations of the directrices are
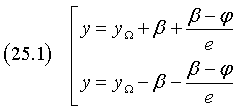
3.3 Hyperbolas
If (B = 0) ∧ (AC < 0), from the (7) the (1) is the equation of a hyperbola. We have the following particular cases.
(B = 0) ∧ (A > 0) ∧ (C < 0) ∧ (A+C < 0) ⇒ (a ≠ 0) ∧ (b = 0): the (1) becomes
![]()
The conic is a hyperbola with directrices parallel to the y axis and a focal axis parallel to the x axis.
By completing the squares
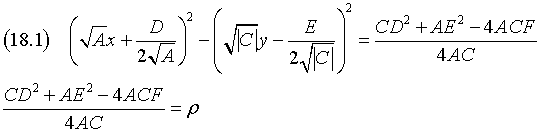
If ρ is not positive, the hyperbola is not real. Otherwise it has center Ω and semiaxes α and β
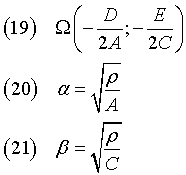
The distance φ of the foci from the center Ω and the eccentricity e are
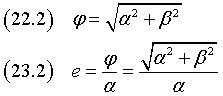
The coordinates of the foci Φ1 and Φ2 are
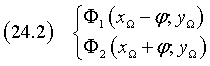
Let P and Q be the points of intersection of the conic with the focal axis (xP < xQ) and H and K the points of intersection of the focal axis with the directrices (xH < xK); we have
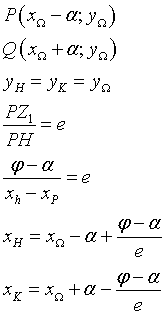
Therefore the equations of the directrices are
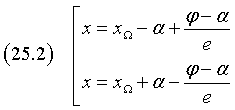
(B = 0) ∧ (A > 0) ∧ (C < 0) ∧ (A+C > 0) ⇒ (a = 0) ∧ (b ≠ 0): la (1) becomes
![]()
The conic is a hyperbola with directrices parallel to the x axis and focal axis parallel to the y axis.
By completing the squares
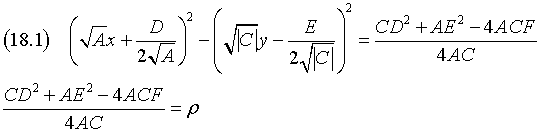
If ρ is not positive, the hyperbola is not real. Otherwise it has center Ω and semiaxes α and β
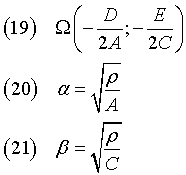
The distance φ of the foci from the center Ω and the eccentricity e are
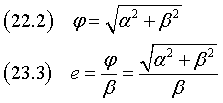
The coordinates of the foci Φ1 and Φ2 are
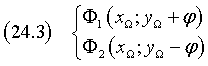
Let P and Q be the points of intersection of the conic with the focal axis (yP > yQ) and H and K the points of intersection of the focal axis with the directrices (yH > yK); we have
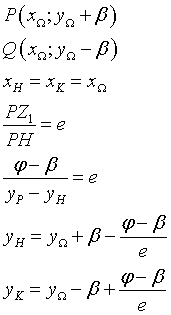
Therefore the equations of the directrices are
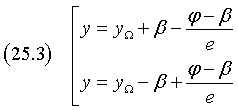
If B ≠ 0, for the third one of (2), a, b and e are all ≠ 0: directrix and axis of symmetry are oblique with respect to both Cartesian axes.
In this case, to calculate the characteristics of the conic, we rotate the Cartesian Oxy reference system by an angle θ so that the equation of the conic in the rotated OXY system has the coefficient B equal to 0, thus obtaining one of the situations examined in the previous section.
Representing the coordinates in the rotated system with capital letters and with θ the angle of rotation, the equations of the rotation R are
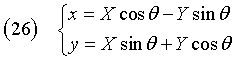
From (1) we have
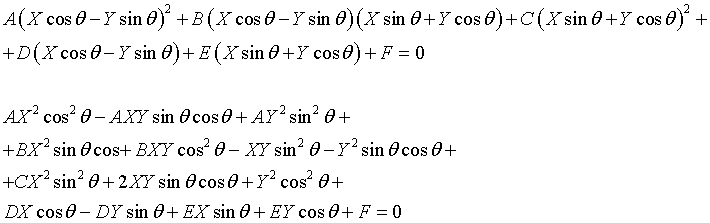
Rearranging in decreasing powers of X and Y
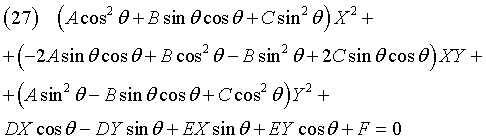
The coefficient of the monomial in XY must be = 0:
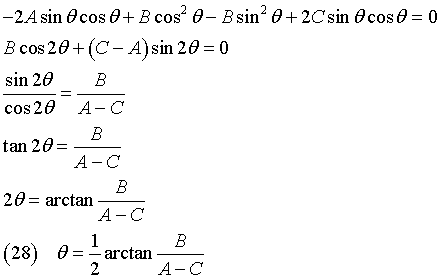
Given θ, we can calculate the other coefficients
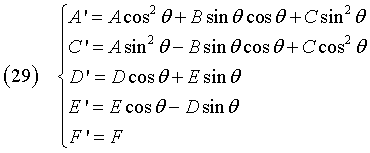
The (27) becomes
![]()
We can then apply to this equation the analysis made in section 3 for the equation (1) when in it B = 0 and A=A', C=C', D=D', E=E', F=F'.
Eccentricity and segment lengths calculated in the OXY system coincide with the corresponding ones in the Oxy system, while the coordinates of the points and the equations of the lines in the Oxy system must be obtained from the corresponding ones in the OXY system by subjecting them to rotation (26).
The following Javascript application, given the coefficients A, B, C, D, E, F, calculates the parameters of the conic and generates the graph.
The coefficients can be written as integers, reals in fixed or floating point or as fractions.
The application works appropriately only if your browser allows Javascript and popup windows.
last revision: September 2018