(from Didactic hints)
In a Cartesian plane xOy an equation with form
![]()
represents an ellipse with axes parallel to the Cartesian axes, center C(α;β) and semiaxes a e b.
The denominators in (1) are intrinsically positive. To simplify the notation and the calculation we represent them with positive parameters
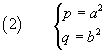
and rewrite the equation in the following way
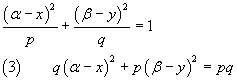
Since in equation (3) there are four parameters (p, q, α, β ), four independent conditions are sufficient to completely determine the equation of the ellipse.
In particular, given four unaligned points P, Q, R, S:
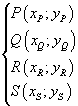
the equation of the ellipse through the four points can be determined by imposing that their coordinates satisfy the equation (3), that is, by solving the system
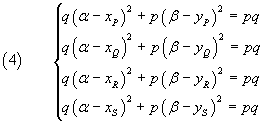
The resolution of the system can be made easier if we observe that, by subtracting side to side the second equation from the first one, we get
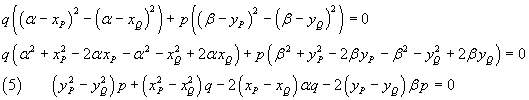
To obtain a linear form, in the equation (5) we set
![]()
then
![]()
The same procedure can be applied to any other pair of equations of the system (4), obtaining, for example,
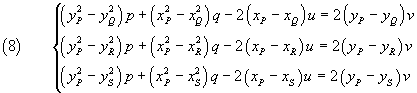
The system (8) allows you to express p, q, u and, consequently, also α and β, as functions of v. By substituting these expressions in any of the equations of the system (4), we can determine v and then the values of p, q, α and β.
The following Javascript application automates the solution of the problem. If the coordinates of the points are rational (ie do not contain the decimal point, but can contain a slash), also the parameters a, b, α and β are expressed by rational numbers.
The applet calculates equation, center and semiaxes and can produce the graph of the ellipse.
last revision: September 2018