The area of a parabolic segment

1. Definitions

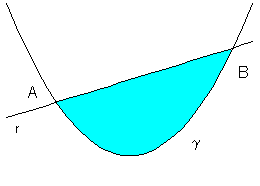
Given in a plane Π the parabola γ and the straight line r which intersects γ in two different points A and B, the finite portion of Π delimited by the arc AB and by the chord AB is said parabolic segment.

figura 1

In particular, if the straight line r is perpendicular to the axis of γ, it is a right parabolic segment.

figura 2

otherwise, like in the first figure, it is an oblique parabolic segment.

2. How to approximate the area

In order to calculate the area of a right parabolic segment, we can adopt the following way.

We represent γ in a cartesian orthogonal reference system Vxy with origin in the vertex V of γ and with the ordinate axis coincident with the symmetry axis of γ. In this reference system the equation of γ is
Let B' be the projection of B on the abscissa axis and l the length of OB'. Let's divide OB' in n equal segments. The abscissa of the right ends of these segments will be
Let's construct n rectangles having base on each segment and altitude given by the ordinate corresponding on γ to the abscissa of the right end of the base.
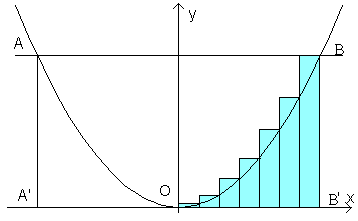
The i-th rectangle has area
The sum R of these areas is
The bigger n is, the lesser is the difference between R and the area S of the figure delimited by the segments OB' and B'B and by the arc OB of γ (a mixtilineal triangle). We can express this asymptotic tendency saying that

3. The sum of the squares of the first n natural numbers

The following table shows that the sextuple of the sum of the first n natural numbers can be easily expressed by the product between the last number, its successive number and the successive of its double

i	i²	Σ i²	6 Σ i²	6 Σ i²
1	1	1	6	1 · 2 · 3
2	4	5	30	2 · 3 · 5
3	9	14	84	3 · 4 · 7
4	16	30	180	4 · 5 · 9
5	25	55	330	5 · 6 · 11

By induction, it can be proved that

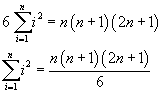
figura 9

4. Archimede's theorem.

With this result, we can rewrite R in the following way

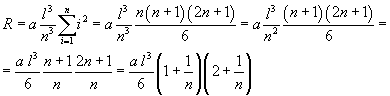
figura 10

As n approaches infinity, 1/n approaches 0, therefore

that is the area S is one-third of the area of the rectangle with base OB' and altitude B'B. Consequently the remaining part of the rectangle is two-thirds of its area.

By the symmetry of the figure we can conclude that the area of a parabolic right segment is two-thirds of the area of the circumscribed rectangle. This property is commonly referred as Archimede's theorem.

5. The oblique parabolic segment.

If a parabolic segment is defined by the intersection of a parabola γ of equation y=ax² (a>0) with the straight line r, oblique with respect to the axis of &gamma, its area can be obtained by the difference between the area of the trapezoid ABB'A' and the areas of the mixtilineal triangles S₁ and S₂.

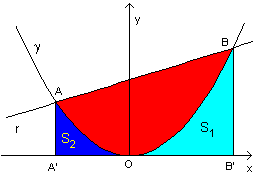
Let x_A and x_B (x_A<0<x_B) be the abscissas of A and B. The segment AB has measure , the segment AA' has measure and the segment BB' has measure .

The area of the trapezoid is therefore

The area of the mixtilineal triangle S₁ is one-third of that of the rectangle with sides OB' and BB' and the area of the mixtilineal triangle S₂ is one-third of that of the rectangle with sides OA' and AA', that is

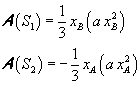
The area of the parabolic segment AOB is therefore

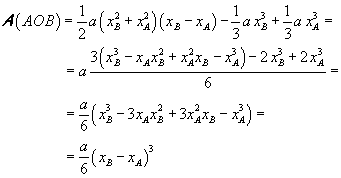
This expression of the area can be applied to every parabola with equation (a>0). In fact such parabolas can be obtained by translations which doesn't change the distances and the parameter a.

Obviously, if a is negative, we must take the absolute value of a.

In conclusion, given a parabola of equation intersected by a straight line in two points A and B, the parabolic segment bounded by the chord AB and the arc AB has area

last revision: November 2016