(notes by R. Bigoni)
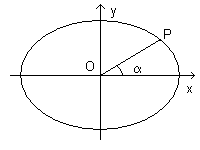
From the canonical equation of the ellipse we can easily deduce the expressions of the cartesian coordinates of a point P of the ellipse as functions of the angle α formed by the vector OP (where O is the origin of the reference frame) and the abscissa axis.

In fact, if we let
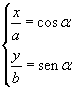 and
square both the sides of both equations, by summing the squared equations we obtain the
canonical equation
and
square both the sides of both equations, by summing the squared equations we obtain the
canonical equation
![]()
So we have
![]()
which are the parametric equations of the ellipse.
The parametric equations of x e y can be respectively interpreted as the abscissa and the ordinate of the points A and B intercepted by the ray, starting at O and forming the angle α with respect the x-axis, on the concentrical circumferences with radii a and b.
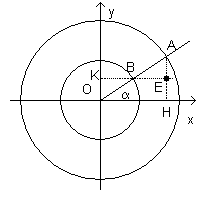
The point E in the figure, which has the same abscissa as A and the same ordinate as B, is a point of the ellipse with semiaxes a and b.
The ordinates yE e yA of the points E and A are
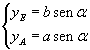
so we have
![]()
that is the ratio between the ordinate of the point E of the ellipse with semiaxes a and b and the ordinate of the point A with same abscissa of the circumference with same center and radius a is b/a.
If, considering for simplicity sake only the points with positive ordinate, for each point E and A we construct the rectangles on the same base dx and altitudes yE e yA, the former rectangles have area b/a with respect to that of the latter ones.
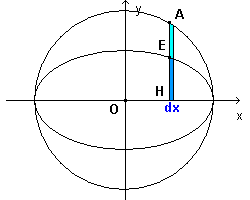
Consequently, the sum of all the first rectangles is b/a with respect to the sum of the second ones. If dx is infinitesimal, the first sum is the area of half the ellipse, the second one is the area of half the circle. In conclusion, the area of half the ellipse is b/a with respect to the area of half the circle and, obviously, the area of the ellipse is b/a with respect to that of the circle.
![]()
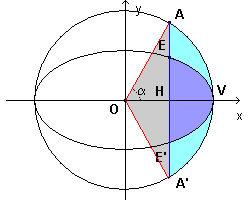
A straight line parallel to the y-axis with equation
![]() delimitates the figure EE'V (colored in blue), which is said elliptical right
segment. The area ε of this figure is
b/a with respect to the area η of the circular segment
AA'V.
delimitates the figure EE'V (colored in blue), which is said elliptical right
segment. The area ε of this figure is
b/a with respect to the area η of the circular segment
AA'V.
The area η in its turn can be obtained by subtracting from the area σ of the circular sector AOA'V the area τ of the triangle AOA'
The area σ is to circle area as its central angle AOA' is to full angle, that is as its half α=AOV is to the straight angle.
![]()
The area τ measures
![]()
therefore the area η measures
![]()
and the area ε measures
![]()
In order to express this area as function of h, we notice that
![]()
therefore
![]()
Example.
Given the ellipse γ with semiaxes a=4 and b=3, the areas of the elliptical segments, obtained by cutting γ parallelly to minor axis at the distance h=2 from it, have measures
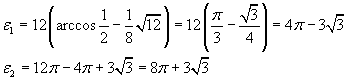
We can demonstrate that the perimeter of the ellipse with semimajor axis a and eccentricity e is
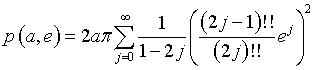
The following Javascript application allows you to approximate the perimeter of the ellipse.