(Notes by R. Bigoni)
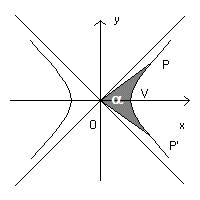
From the canonical equation of the hyperbola you can immediately deduce the expressions of the coordinates of an its point P in the first quadrant as a function of a common variable represented by the area α bounded by the segment OP (where O is the origin of the canonical system), by the segment OP' (with P' symmetric to P with respect to the abscissa axis) and by the arc PP' of the hyperbola itself. If the point P is in the fourth quadrant, α must be assumed negative.

In fact, if you let
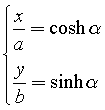
squaring both sides and subtracting side by side you get the canonical equation
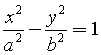
Therefore
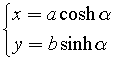
These are the parametric equations of the hyperbola.
By varying the parameter α from -∞ to +∞ you get the coordinates of the points of the arc of hyperbola in the first and fourth quadrant. The arc in the second and third quadrant is its symmetric.