(notes by Roberto Bigoni)
A conic γ with eccentricity e and parameter p, in the cartesian orthogonal reference system Fxy with origin in its focus F and with abscissa axis coincident with its symmetry axis and oriented outward with respect to its directrix, is described by the equation
![]()
equivalent to
![]()
If the points P(xP;yP) and Q(xQ;yQ) belong to γ, from the (1) we have
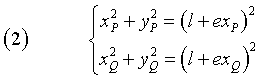
By subtracting term by term the first equation from the second one, we have
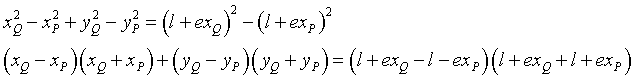
![]()
The slope of the straight line PQ is
![]()
that is
![]()
If we substitute this expression in the (3) we have
![]()
and, by simplifying,
![]()
from which
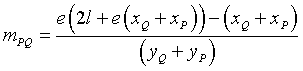
The slope of the tangent to γ at P is the limit of mPQ when Q→P:
![]()
Therefore the equation of the tangent to γ at P is given by the equation of the pencil of straight lines through P setting the slope to (6)
![]()
By expanding and rearranging the (7) we obtain
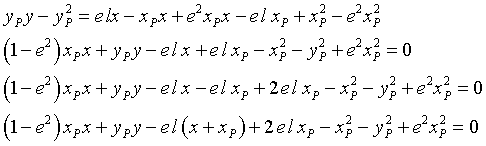
From the first one of the (2) we have also
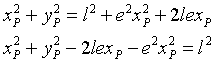
therefore the equation of the tangent to γ at P(xP;yP) is
![]()
If we compare the equation (8) of the tangent at P with the equation (1.1) of the conic, we see that the (8) can be directly deduced from the (1.1)