A property of the ellipse.

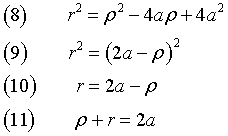
(notes by R. Bigoni)

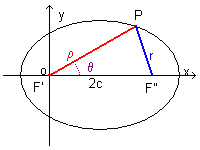
Let P be a point on the ellipse ε and let F' and F'' be the foci of ε

It can be demonstrated that the sum of the measures of the segments PF' and PF'' is equal to the measure of the major semiaxis of ε, that is 2a.

Let ρ be the measure of the segment F'P, r that of the segment F''P and 2c that of the segment F'F''.

Let's consider the triangle F'F''P. From the law of cosines we have

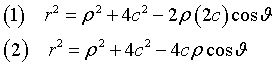
Since c = a e

From the polar equation of ε we obtain

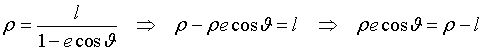
and, by substituting this in the (3)

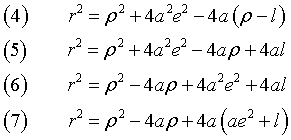
Finally, remembering that

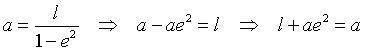
we can deduce that