(notes by R. Bigoni)
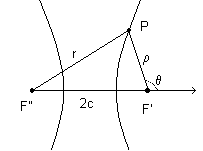
Let γ be a hyperbola with semimajor axis a and focuses F' and F'' and let P be a point of γ. It can be demonstrated that the absolute value of the difference between the distances from P to F' and from P to F'' is equal to the measure of the major axis 2a.

With reference to the figure, let 2c be the measure of the segment F'F'' and let P be a point on the right branch, that which has the vertex closer to the focus F'. Let ρ be the measure of the segment F'P and r the measure of the segment F''P.
By applying the cosine rule to the triangle F'F''P we obtain
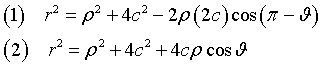
Since c = a e we have
![]()
From the polar equation of the conic (2.2) we obtain
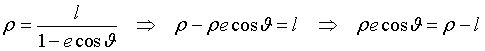
so the (3) can be rewritten as
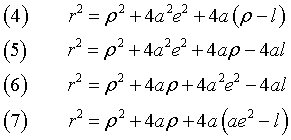
Finally, using the expression of a in terms of e and l
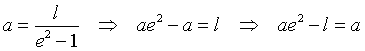
we have
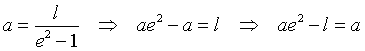
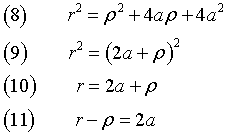
Since the symmetry of the hyperbola, if the point P belongs to the other branch of the curve, that which has vertex closer to the focus F'', we can obtain
![]()