,
reduced to lowest terms, a finite sequence of natural numbers
can be obtained in the following way(notes by R. Bigoni)
A rational number, by definition, is representable by a fraction, ie the quotient between two integers. In fact, the term rational derives from the Latin word ratio, which means quotient.
From each positive fraction ,
reduced to lowest terms, a finite sequence of natural numbers
can be obtained in the following way
where a0 is the maximum natural number
≤ , ie the integer part of the quotient
of n divided by d, r0 is the integer remainder of this division and d0
coincides with the denominator d.
For example: 
. In this case
a0=2 and r0=3.
If r0 is equal to 0, that is if the numerator is a multiple of the denominator, the procedure terminates. Otherwise, from (1) we have
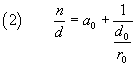
Obviously d0 is greater than r0, and the fraction
can be processed like the fraction , that is
where a1 is the integer quotient of d0 divided by r0 and r1 the remainder of this division. From (2) and (3) we get
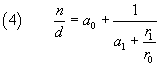
In the above example, we have
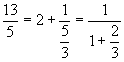
Again, if r1 is equal to 0, the procedure ends. Otherwise, from (4) we obtain
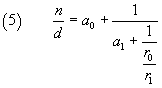
Similarly to the previous cases, 
can be written as
where a2 is the integer quotient of r0 divide by r1 and r2 the remainder of this division.
From (5) and (6) we get
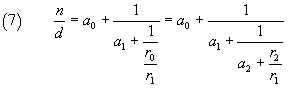
In the above example, we have
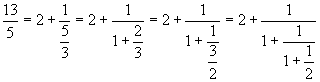
In this example we can see that r2, the last obtained remainder, is equal to 1. When the remainder is 1, the next remainder obviously will be 0, so we can stop the procedure assuming the previous remainder as last term an of the sequence . In the example we havea3=2. As long as the rest is other than 1, the procedure must be repeated.
In the example, we have seen that from the fraction 
we get the sequence [2;1,1,2]. This sequence is said the continued fraction expansion of the fraction
.
The elements of the continued fraction expansion can be quickly obtained from the euclidean algorithm to calculate the greatest common divisor of two natural numbers, recording at each step the successive quotients, while the remainder is greater than 0.
| 13 | 5 | 3 | 2 | 1 |
| quotient | 2 | 1 | 1 | 2 |
| remainder | 3 | 2 | 1 | 0 |
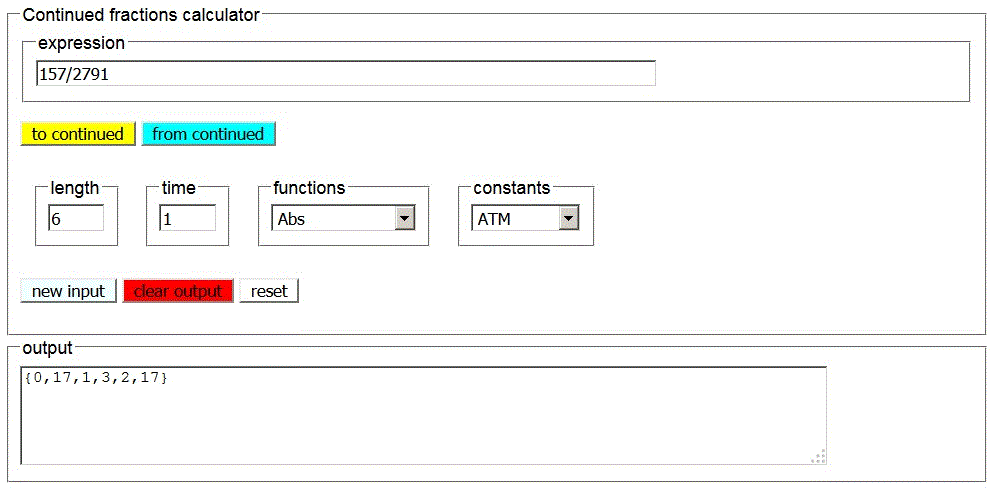
A slightly more complicated example: 
| 157 | 2791 | 157 | 122 | 35 | 17 | 1 |
| quotient | 0 | 17 | 1 | 3 | 2 | 17 |
| remainder | 157 | 122 | 35 | 17 | 1 | 0 |
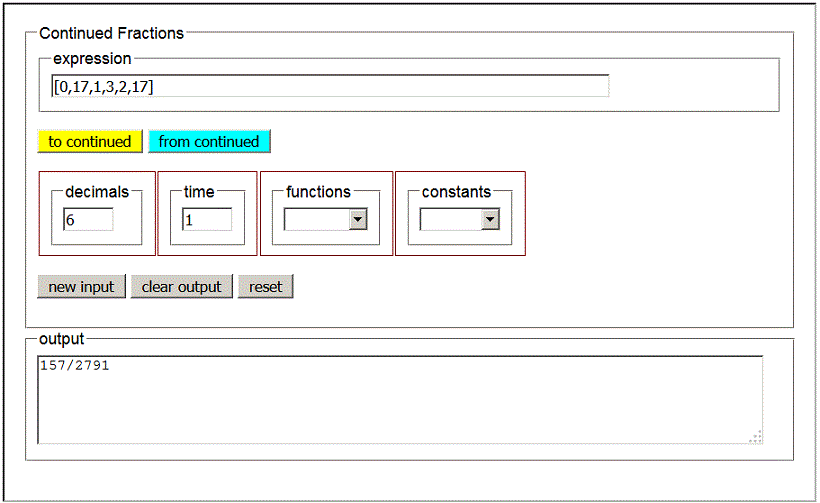
Therefore the continued fraction expansion of is
[0; 17, 1, 3, 2, 17].
This second example shows an interesting property: in the expansion of a fraction less than 1, the first term is 0 and the following terms coincide with those of its reciprocal.
Given a continued fraction expansion, the generating fraction can be obtained by reversing the procedure previously exposed: we must calculate the reciprocal of the last term of the expansion and add it to the previous term; next we calculate the reciprocal one of this sum and add it to the previous term and so on until the first term is reached. Taking the first example above, we have:
With the second example, we have:
The following JavaScript application may be useful to calculate the continued fraction expansion and to do the reverse operation.
The button to continued expands a number, written either as fraction or as decimal number.
The button from continued performs the inverse operation.
The field length allows you to set the maximum number of elements of the expansion.
Examples.
to continued
from continued
An irrational number, by definition, can not be represented by the ratio between two integers, then we can not apply the Euclidean algorithm to an irrational number to obtain its expansion as finite continued fraction, for the same reason, for which we can not obtain a finite representation of the number whichever is the basis adopted. It is known that the decimal representation of an irrational number is a non-repeating decimal number, but, if we wanted to represent it in base two, we would obtain a non-repeating binary number, or, if we wanted to represent it in base sixteen, we would obtain a non-repeating hexadecimal number. However, at least in some cases, is quite simple, using a procedure analogous to that used for the rational numbers, deduce its expansion as infinite continued fraction.
Let us consider, for example, the square root of two, which was the first irrational number discovered in the history of Western mathematics within the Pythagorean school. We have
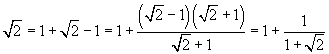
So
If we recursively apply this identity to the roots of two within the denominators, we get
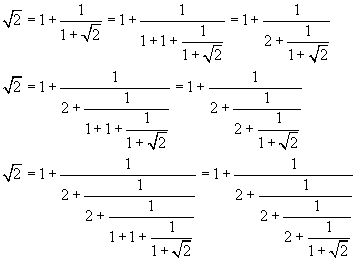
Obviously this recursive procedure can always be repeated, so the procedure does not end, but it is not hazardous to say that the continued fraction expansion of the square root of two is
The square root of 2, which, when represented in base ten, is a non-repeating decimal, when developed as a continued fraction has an infinite repeating expansion.
Another very interesting example is given by the golden number Φ. We have
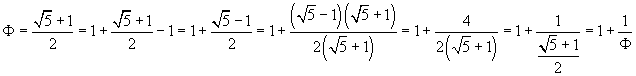
Then
If we recursively apply this identity to the numbers Φ within the denominators, we get
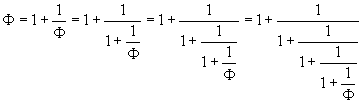
Therefore the expansion of Φ as a continued fraction is
In general, for any real number x:
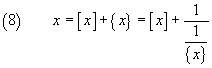
where [x] is the maximum integer number ≤ x, that is its integer part,
and {x} = x-[x] is its fractional part. If the fractional part is greater than 0,
the reciprocal 
is a real number
greater than 0 that, at its turn, can be expressed as the sum of its integer and fractional parts.
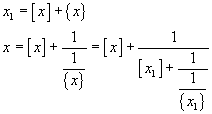
If we represent by xi+1 the reciprocal of the fractional part of xi, we can endlessly repeat this procedure and obtain, at every step, a new term of the infinite sequence of the integer parts of the numbers xi; so the expansion of x as a continued fraction is
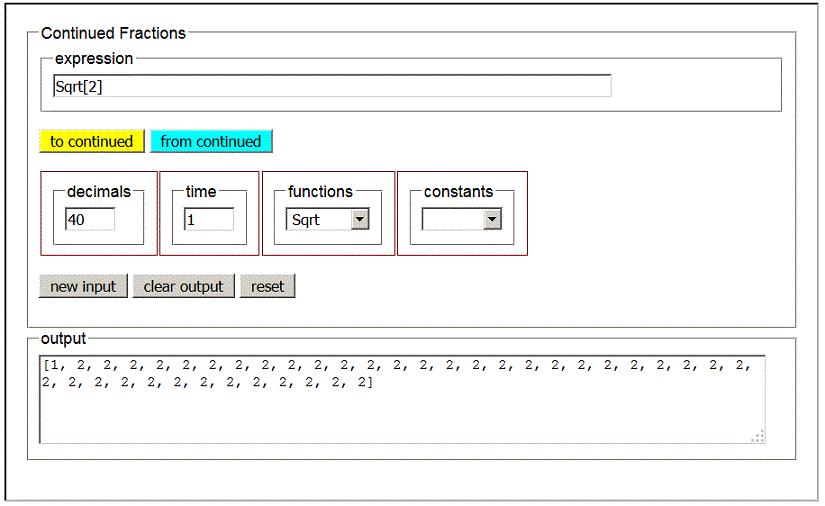
If you want to use the calculator in section2 to obtain the continued fraction expansion of the square root of 2,
it makes no sense to write as input a decimal approximation to it, for example 1.41421356,
because you would get the expansion of a rational number that would be finished.
You can, in this and similar cases, use the selector functions that brings into input one of the names of the most used real variable functions.
You can also use the selector constants, that brings into input one of some of the best known real constants such as e, π and Φ.
Examples.
√2
Φ
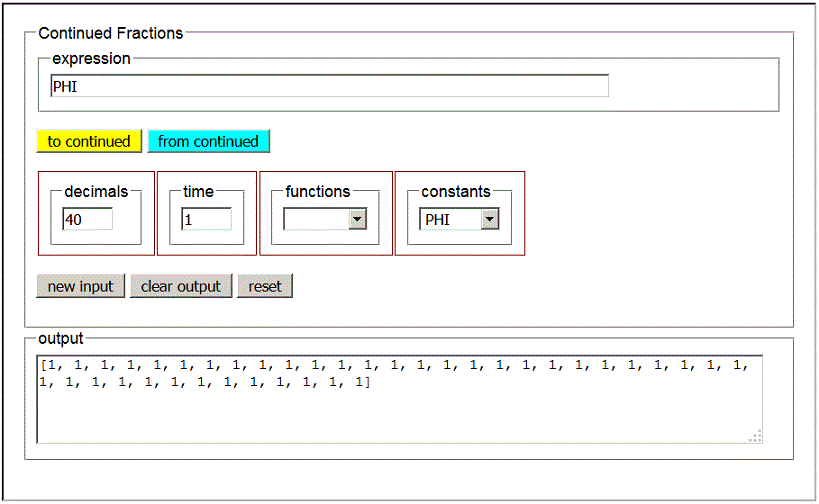
from continued, applied to an inevitably limited development of Φ, produces a rational approximation to Φ.
The same results can be obtained with Mathematica, if you have installed this software, or free with WolframAlpha (documentation), which allows you to use some features of Mathematica.
In general, the expansion of an irrational number as a continued fraction is a good way to obtain a rational approximation
to the number itself. For example, the number Φ, which can be approximated by the quotient between a number of the
Fibonacci sequence and the previous one, with better approximations
as we go on the Fibonacci sequence, can also be approximated at will from its continued fraction expansion, consisting
of an infinite sequence of 1. We can also take this fact to define Φ: it is the number represented by
, where the line over the second 1
indicates its periodicity.
The same applies to 
.
In general, the square roots of natural numbers have periodic expansions.
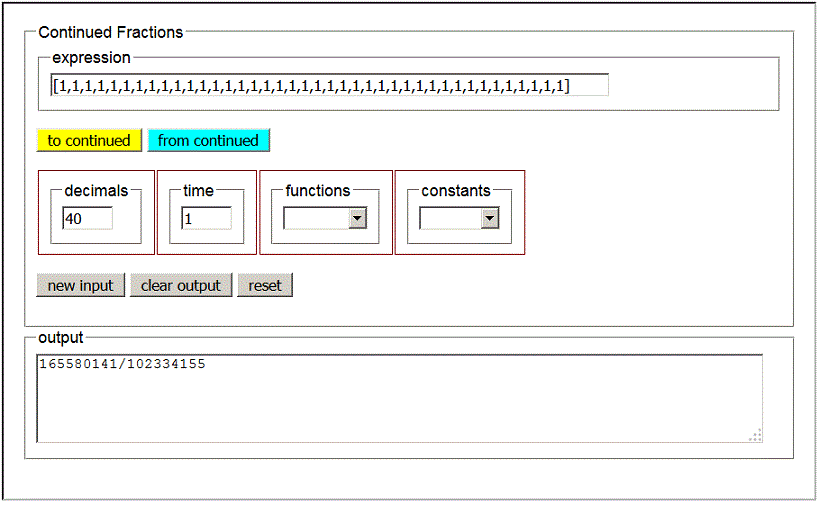
This is quite easy to prove if the radicand is the number immediately following a square. In fact
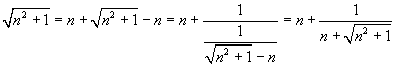
then
By recursively applying the identity (10), we obtain
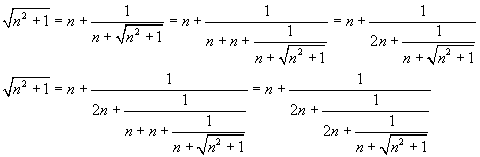
In conclusion
From (11)
If the radicand exceeds the square of a natural number of 2 units, we obtain
then
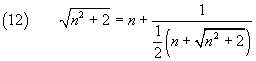
By recursively applying this identity, we obtain
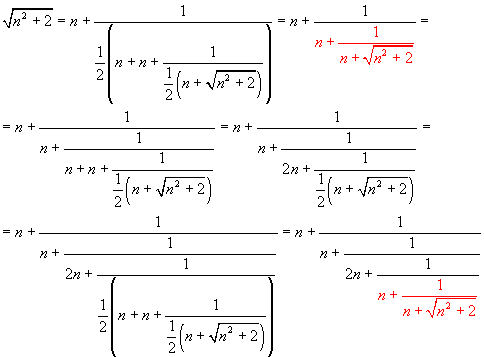
The last obtained denominator coincides with that of the first line, so the cycle repeats regularly. In conclusion
From (13)
Conversely, a repeating continued fraction can be expressed by the solution of a quadratic equation with natural coefficients.
Example: a fraction with two repeating digits.
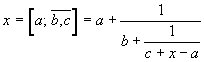
The number x is given by the positive solution of the equation
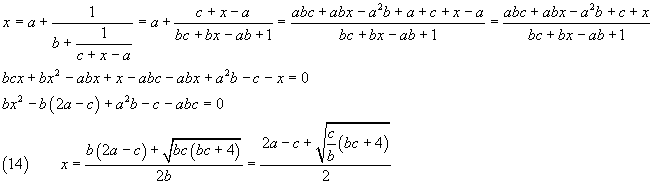
From (14) we obtain particularly simple cases for c=2a and multiple of b. Examples:
From (9), if we assume x=cotanh(1) and use a calculator, we get
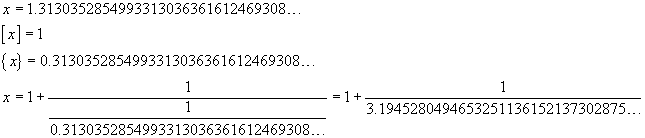
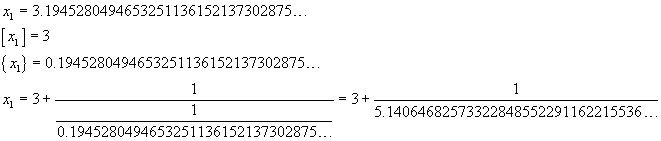
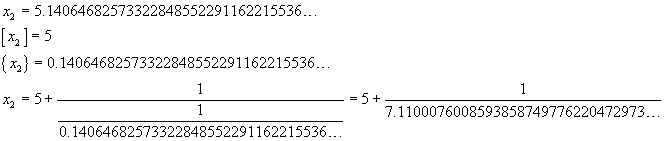
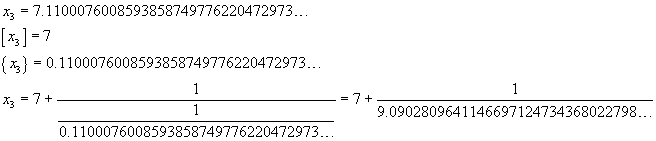
If you use the calculator in paragraph 2, you get get
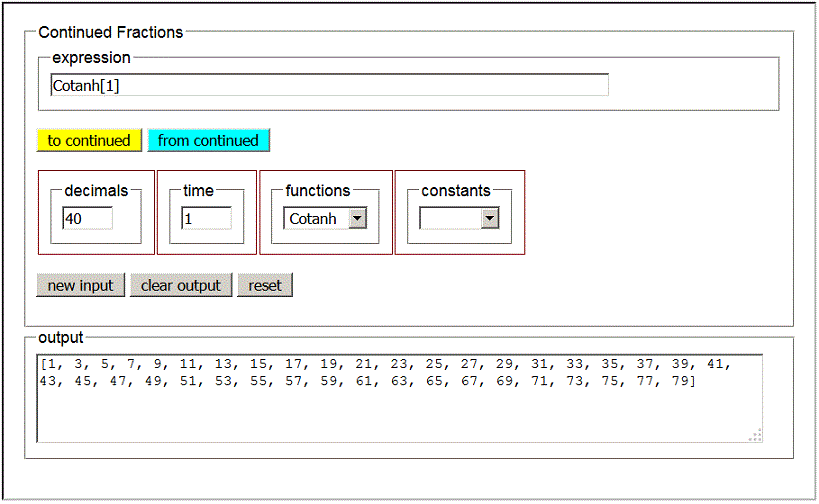
Obviously, the continued fraction expansion of cotanh(1) is not periodic, but it shows a remarkable regularity: we can conjecture that it is given by the sequence of the odd numbers.
In fact, the conjecture is correct, and has been demonstrated by Euler.
The base E of the natural exponential, ie the Euler'number.
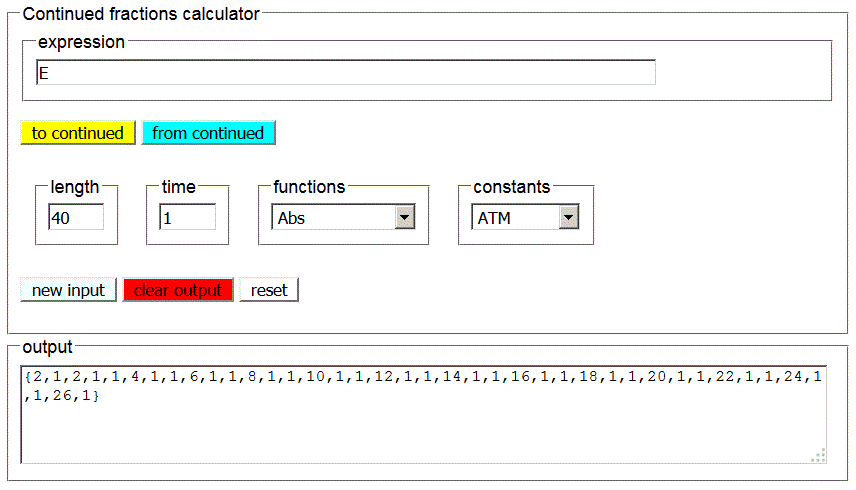
Also in this case we can note a clear regularity: from the third term forward, we see the even numbers followed by a pair of 1. We may conjecture that the continued fraction expansion of e is
If we suitably extend this sequence and calculate the generating fraction, we can approximate e with the desired precision. This method of approximation can be a viable alternative to the Maclaurin series expansion.
last revision: May 2018