Binomial integrals

(notes by Roberto Bigoni)

In this page we shall call binomial integrals definite integrals of the form

because in these integrals the integrand is an integer power of a binomial. This power can be easily expanded

so, if we integrate this expansion from 0 to 1, we obtain

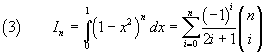
If we now calculate the first values of these expansions we have

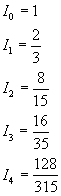
and we can observe that

It is therefore natural to conjecture that, in general, for every natural number n greater than 0,

In particular

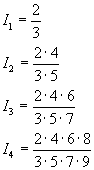
In general

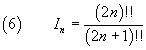
In (6) the double exclamation mark represents the double factorial of the number before it. As you can see from the examples, if a number is even, its double factorial is the product of the number itself by all the even numbers less than it; similarly, if the number is odd, its double factorial is the product of the number itself by all the odd numbers less than it.

In the page on the mathematical induction you may see a demonstration of (6) based on the fact that I_n can be expressed also in the following way

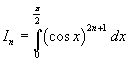
In conclusion, for every natural number n we have

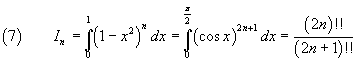
Last Revised: May 2018