Gaussian Integrals

(edited by Roberto Bigoni)

The integrals of the form

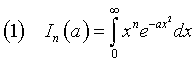
which are frequently encountered in the probability theory, considered as functions of a, have the following recursive property

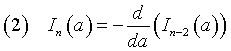
that is

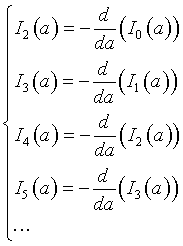
Therefore, if we know I_o(a) and I₁(a), we can calculate any other I_n(a).

• The calculation of I₁(a) is quite easy.
  In this case the integrand function

  

  is the derivative with respect to x of

  

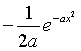
  so

  

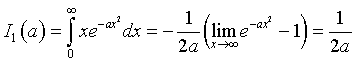
• The value of I_o(a), in which the integrand function is the exponential function

  

  can be obtained in the following way:

  1. we consider twice the integral of this function on the whole ℜ, using two variables x and y

     

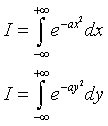
     therefore

     

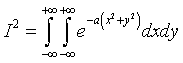
  2. in the plane Oxy we substitute the polar coordinates (ρ,θ) to the Cartesian coordinates (x,y):

     

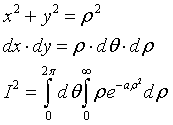
  3. the first integral of the product has value 2π, the second is I₁, therefore

     

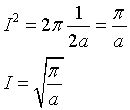
  4. Due to the symmetry of the Gaussian function, the value of I₀ is half of this value, therefore

     

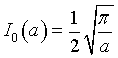
Finally we can obtain from (2)

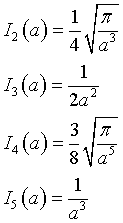
and so on.

In general

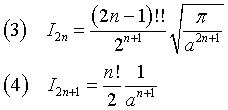
that is

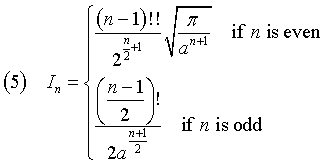
last revision: May 2018