10. Functions as vectors.

If the elements of a given set are such that they can be submitted to the same operations we can do on n-dimensional real vectors, they are vectors and the set is a vector space.

This statement can be verified in particular for some set of functions of a given form.

Let's consider, for example, the set Σ₂ of the functions with a and b real numbers and defined for x ∈ [-π ; π]. For simplicity sake, these functions will be shortly written σ₂(a,b) and sometime only σ₂.

Whichever two functions of Σ₂ can be summed in the usual algebraic way giving a function of Σ₂, so Σ₂ is closed under the sum. The sum is associative and commutative. The neutral element of the sum is obviously σ₂(0,0) and for every σ₂(a,b) there is in Σ₂ the opposite element σ₂(-a,-b). Therefore Σ₂ with the sum is a commutative group.

σ₂(a,b) can be multiplied by a real number k giving σ₂(ka,kb), so Σ₂ is a vector space.

Moreover, given whichever functions σ₂(a,b) and σ₂(c,d), we have

The Wolfram Integrator speeds the calculation of this and other integrals in these pages.

The value of this integral coincides, apart from the constant factor π, with the scalar product between the real plane vectors (a,b) and (c,d). It seems therefore logical to take this integral as the expression of the scalar product between σ₂(a,b) and σ₂(c,d):

This definition allows to define a norm ||σ₂|| for the vector |σ₂>

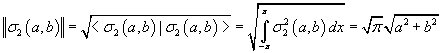
So the set Σ₂, like the set of the real plane vectors, is a normed vector space.

A linear operator L on Σ₂ must transform univocally a vector into another vector in the same space and must have the same properties of the real square matrices with respect to real plane vectors hightlighted in section 2, that is

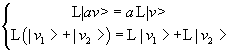
The second derivative of the functions of Σ₂ with respect to the variable x has such properties; in fact the derivative of a sum of functions is the sum of the derivatives of each function and the derivative of the product of a function by a real number k is the product of the derivative of the function by k. Moreover

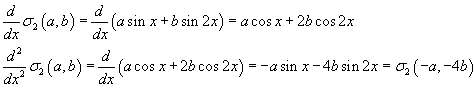
Therefore the double differentiation operator is a linear operator on Σ₂. In order to calculate its eigenvalues and its eigenvectors (here its eigenfunctions) one must solve the equation

that is

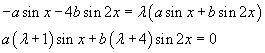
This equation can be satisfied only if

So the eigenvalues of the double differentiation operator are λ₁=-1 and λ₂=-4; the corresponding eigenfunctions are σ_2,1=a sinx and σ_2,2=b sin2x.

Like in real plane vector space, these eigenfunctions can be normalized if we assume that the scalar factor a and b are positive and divide each vector for its norm. We obtain

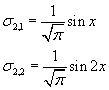
The normalized set {σ_2,1 , σ_2,2} is an orthonormal basis of Σ₂: each of these two functions has norm 1 and their scalar product is 0. All the vectors of Σ₂ are linear combinations of these two functions just like all the plane real vectors are linear combinations of the vectors (1,0) e (0,1).

If we consider the set Γ₂ of the functions defined for x ∈ [-π ; π], we reach analogous results.

The analogy persists also if we consider the set Φ₂ of the functions which are such that .

This integral gives a value that, apart from the constant factor π, coincides with the scalar product of the two 4-dimensional vectors (a,b,c,d) e (h,k,l,m).

By induction, we can infer that Φ_n, that is the set of the functions , is a normed vector space in which the norm is given by .

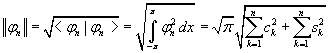In particular, for whichever pair of functions 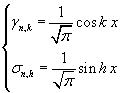we have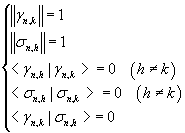

Therefore the union of the sets of the functions is an orthonormal basis of the vector space Φ_n and each function of Φ_n can be expressed in the following way

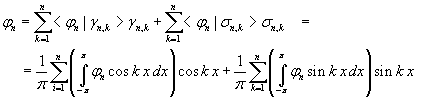
In conclusion, if we let

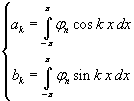
we have