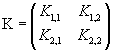
The operator K
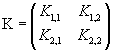
applied to the vector
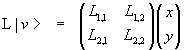
gives the vector
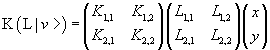
By ordinately expanding the products we have
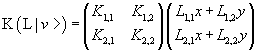
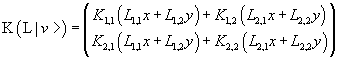
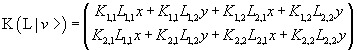
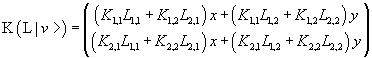
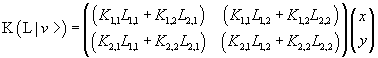
Therefore the application of L and after of K to to the vector v gives the same result of the application of the operator P
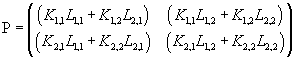
P can be said the product of K and L
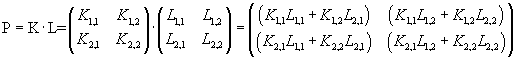
We can see that
the product of two square matrices with the same size is a square matrix with the same size whose entries are the sum of the products between the entries of each row of the first matrix and the corresponding entries of each column of the second matrix.
The product of two matrices isn't commutative: in general KL≠LK.
The product between the matrix I (the identity matrix) and another matrix L gives the matrix L: I is the neutral element of the product between matrices of the same size. I commutes with whatever matrix.
Two matrices with the same number of rows and columns (in particular the square matrices with the same size) can also be summed: their sum is an analogous matrix whose entries are the sum of the corresponding entries in the addends.
The properties here referred to the plane vectors and their matrices can be extended to the real vectors and matrices of any finite dimension and, with some adjustment, also to the field of the complex numbers and to more abstract kinds of vector and linear operators.