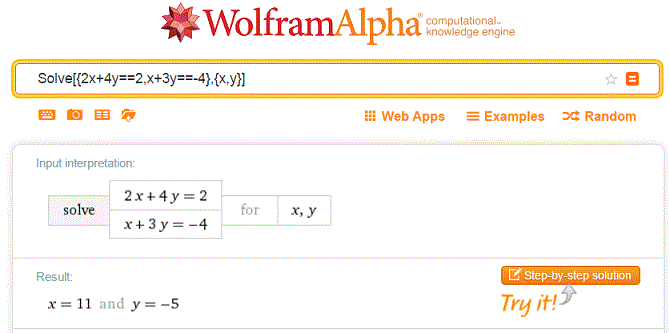
A linear system such
![]()
can be interpreted as
![]()
The problem is to find, if possible, a vector v(x;y) such that the product
between the matrix
![]() and
v(x;y) equates the vector v’(c;c’) or, more syntheticaly,
to solve the equation
and
v(x;y) equates the vector v’(c;c’) or, more syntheticaly,
to solve the equation
![]()
From the elementary algebra we obtain
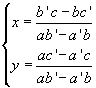
The two fractions can exist only if their denominator isn't null. This denominator, formed only by the coefficients of S, is said the determinant of S.
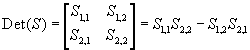
N.B.: In these pages matrices have their entries between parentheses and determinants have their entries between square brackets.
Using Δ to represent the determinant of S, if Δ is not null, we can write
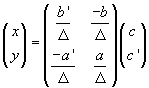
If we call S-1 the operator in the second side, we can say that the solution of the equation
![]()
is
![]()
The product between S-1 and S is the identity matrix. Therefore S-1 is the reciprocal (or inverse) matrix of S.
S admits a reciprocal matrix only if its determinant isn't null.
In general, given a square matrix S, we can find its inverse matrix in the following way.
First, we calculate Δ, the determinant of S.
To calculate Δ we can apply the
Laplace's rule.
Example.
Given the matrix
![]()
we have Δ=2, so the inverse matrix is
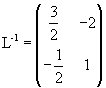
The product between L-1 and L is
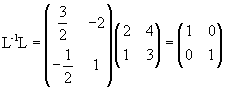
This procedure can be applied to more complex systems of n equations with n unknowns. Obviously, the more n is big, the more the calculations grow, and we need powerful instruments of automatic computation such Mathematica (©Wolfram) or WolframAlpha.