5. Linear operators in plane analytic geometry.

If we interpret a two-dimensional vector v(x_v;y_v) as a point V(x_v;y_v) in the cartesian plane Oxy, the linear invertible operators represented by square 2x2 matrices act as bijective transformations of the point V(x_v;y_v) into a point V'(x_v';y_v') of Oxy. We shall call these transformations geometric linear transformations.

Such transformations show interesting geometric properties.

• They transform the origin O into itself.

  

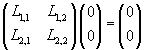
• Given in Oxy the triangle τ with counterclockwise oriented vertices A(x_A;y_A), B(x_B;y_B), C(x_C;y_C), the double area of τ is

  

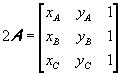
  A geometric linear transformation 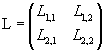transforms the triangle τ into a triangle τ’ with double area

  

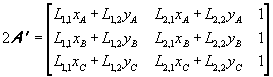
  The determinant in the second side is the product of the determinants

  

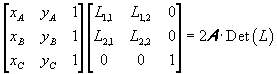
  therefore

  

  A geometric linear transformation L transforms a triangle τ with area A into a triangle τ' with area A' given by the product between A and the determinant of L.

  • Since the geometric area is intrinsically positive, if the determinant is negative one must take its absolute value.
  • Since every polygon may be decomposed in triangles, the theorem can be extended to all polygons.
  • In general the theorem can be extended to all plane figures.
  • Three points are aligned if and only if the determinant is null, therefore if three points are aligned also the transformed points are aligned, that is a geometric linear transformation transforms a straight line into a straight line.

   

• Let we consider two straight lines parallel each other but not parallel to any coordinate axis. Let the first intersects the axes in points U(p;0) and V(0;q), the second in points R(kp;0) and S(0;kq).

  The linear transformation 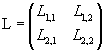transforms these points into the following

  

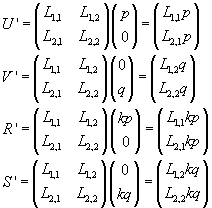
  The slopes of the transformed lines are equal.

  Therefore a linear transformation transforms parallel straight lines into parallel straight lines.

  A linear transformation transforms parallelograms into parallelograms.