A linear operator L on the vector space V can admit a set of vectors which, when transformed by L, result multiplied by a scalar.
Vectors of this set are said eigenvectors li and the corresponding scalars are said eigenvalues λi of the linear operator L.
To compute eigenvectors and eigenvalues of L one need to solve the following equation said eigenvalue equation
From this equation we have
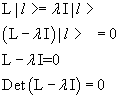
The last equation allows the calculation of the eigenvalues λi. It is easy if the dimension n of the vector space is 2, but difficult if n is greater, because it is equivalent to a polynomial equation of degree n and, in general, it can have complex roots.
However if the matrix of L is diagonal, that is
if all its entries are null except those with equal indices, the equation
is equivalent to
with a trivial set of solutions
.
In this case, the eigenvalue equation is equivalent to the set of equations
which admit solution only if the components of the eigenvector |li> are null except that with index i.
Example.
Given the diagonal matrix
,
one has
that is
therefore
.
The eigenvector |d1>, corresponding to the eigenvalue δ1=a,
is obtained from the equation
,
that is
,
true for all x if y=0. So the calculation doesn't find a determined vector,
but the set of all the vectors laying on the x-axis. In order to determine the result
we select from this set the vector with unitary norm and with the same direction as
the x-axis. This is the normalized eigenvector.
So in the example we have
.
The analogous calculation with respect to the eigenvalue |d2>,
corresponding to the eigenvalue δ2=2, we obtain
.
The results shown in the above example can be generalized to n-dimensional diagonal matrices. Therefore, in general:
From the eigenvalue equation we can deduce that, given the matrix L and another matrix M with its inverse M-1, the matrix M-1LM has the same eigenvalues as L. In fact
In particular this is true if M is a rotation.
If the matrix which undergoes the rotation M is a diagonal real matrix like the D of the example, the transformed matrix S=M-1DM is a symmetric real matrix, that is such that, if i≠j, Si,j=Sj,i. In fact we have
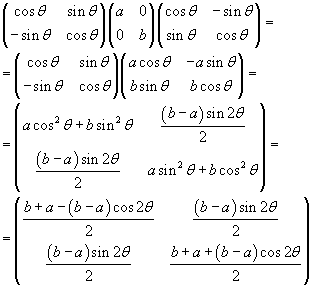
Vice versa, using the opposite procedure, every real symmetric matrix can be transformed in a diagonal real matrix.
In fact, given the matrix
,
in order to find the rotation which diagonalizes S, we let
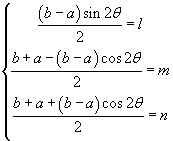
The term by term subtraction of the second equation from the third one gives
From this equation and from the first one we have
Therefore the rotation with angle -θ transforms S into D.
This procedure can be applied to any symmetric real matrix, so we can say that all the eigenvalues of a real symmetric matrix are real values.
Example.
Given the real symmetric matrix
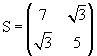the eigenvalue equation is
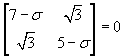from which we have
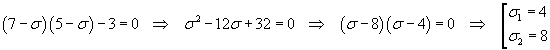
The eigenvalues are σ1=4 e σ2=8.
In order to calculate the corresponding normalized eigenvectors one need to solve the equations
, where
the norm of the vectors |si> is 1, so they can be expressed as
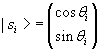with
.
Using the first eigenvalue we have
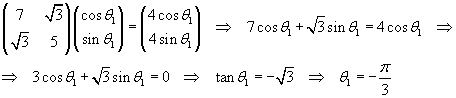
therefore
.
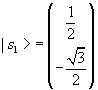Using the second eigenvalue we have
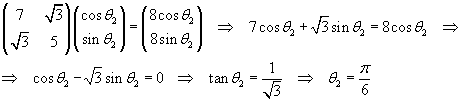
therefore
.
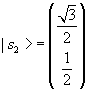The eigenvectors are orthonormal.
There exists a rotation that transforms S into a diagonal matrix with the same eigenvalues
.
The same rotation transforms the normalized eigenvectors of S into the unit vectors of the
cartesian axes. In the proposed example the rotation angle is π/6.
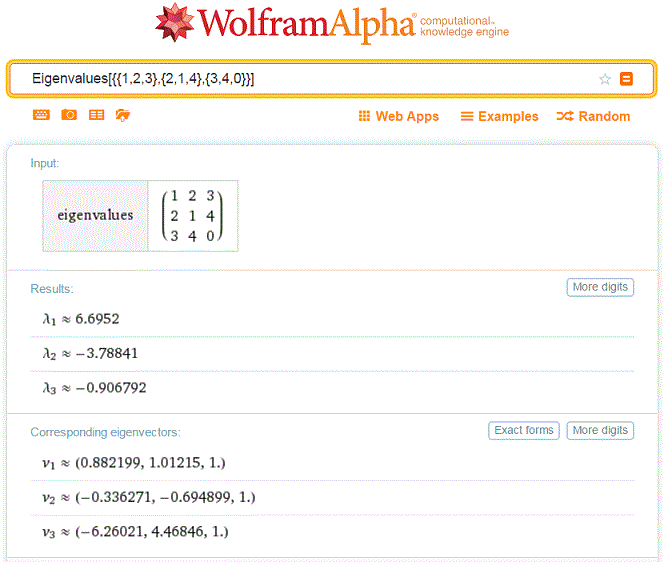
Eigenvalues and eigenvectors with WolframAlpha
