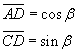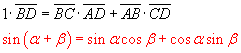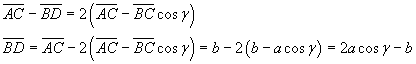Click on the points A, B, C, D to move them, avoiding to alter their counterclockwise order.
Ptolemy's theorem
(note by R. Bigoni)
A theorem of the classical plane geometry which may be a useful bridge to some of the most important
theorems of the trigonometry is the so called Ptolemy's theorem:
In un quadrilateral inscribed in a circle the product of the measures of its diagonals equals the
sum of the products of the measures of the opposite sides.
Demonstration (see 'cut-the-knot')
Thesis: 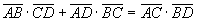
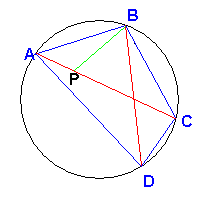
Let P be the point of the diagonal AC such that the angle APB is equal to the angle DBC.
The triangle APB is similar to the triangle BDC because also the angles BAP and BDC are equal since they
are angles at the circumference subtended by the same arc BC.
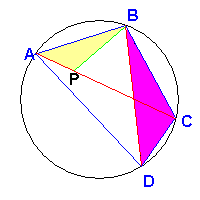
The corresponding sides are in proportion, so
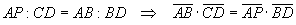
Also the triangles BPC e ABD are similar because the angles PBC and ABD are equal, since they are sum
of equal angles and PCB e ADB are equal since they are subtended by the same arc AB.
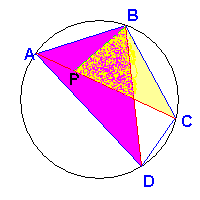
The corresponding sides are in porportion therefore
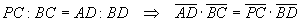
The sum side by side of these two equalities gives the thesis.
From the Ptolemy's theorem we can easily deduce the Pythagoras' theorem.
Indeed, every rectangle is a quadrilateral inscriptible in a circumference and its diagonals coincide with diameters.
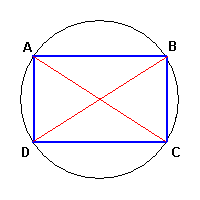
The application of the Ptolemy's theorem to the rectangle ABCD, gives immediately
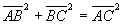
that is, in the right-angled triangle ABC the sum of the squares of the catheti equals
the square of the hypotenuse.
Let the quadrilateral ABCD be inscribed in a circumference and such that its diagonal AC
has length 1 and coincides with a diameter.
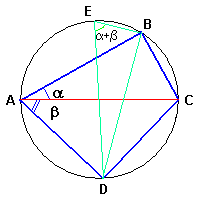
The triangle ACB is right-angled, so
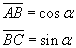
The triangle ACD is right-angled, so
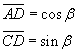
If we draw the diameter DE and the chord EB, we obtain the triangle DEB which is right-angled
and such that the angle DEB is equal to the angle BAD since both are angles at the circumference
subtended by the same arc BD. We have therefore
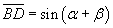
If we now apply the Ptolemy's theorem to the quadrilateral ABCD we obtain
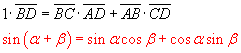
This is sine addition formula from which we can deduce
many other identities.
Let ABC be a triangle with sides a, b e c; let γ be the angle ACB;
let we draw the circumference
circumscribed to ABC and draw from a vertex, for example B, the parallel to the opposite side and let D be
the point in which this parallel intersects the circumference; finally, let we draw the segment DC to
obtain the quadrilateral ABDC.
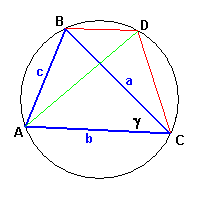
The quadrilateral ABDC is an isosceles trapezoid in which the oblique sides are equal and the diagonals
are equal.
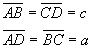
Furthermore we have
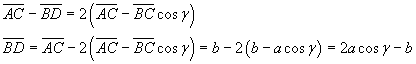
The application of the Ptolemy's theorem gives
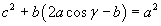
and finally
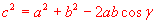
This is a very important equality, more general than the Pythagoras' theorem since it may be applied
not only to right-angled triangles.
In any triangle the square of a side equals the sum of the squares of the other two sides diminished
by the double of the product of the latter two sides and the cosine of the angle between them.
This equality is known as the cosine rule.
last revision: June 2015
![]()


![]()

![]()