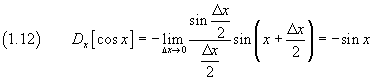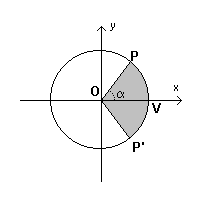

Given in the cartesian plane xOy the graph of the circumference γ
with center in the origin O and unitary radius, whose equation is
![]() ,
let V be the point where it intersects the positive semiaxis of abscissas
and P(x;y) any of its points.
The coordinates x and y of P are functions
of the angle α=VOP and of the length of the arc VP; if this angle is measured
in radians, the measure of this arc numerically concides with that of α.
,
let V be the point where it intersects the positive semiaxis of abscissas
and P(x;y) any of its points.
The coordinates x and y of P are functions
of the angle α=VOP and of the length of the arc VP; if this angle is measured
in radians, the measure of this arc numerically concides with that of α.
If we call P' the point of γ symmetrical of P with respect to the x axis, even the area of the circular sector P'OP numerically coincides with α.
We can therefore interpret the coordinates of P as parametrical functions of the area of the circular sector P'OP.
These functions are said respectively circular cosine and sine of α.
So we have
![]()
and, by the equation of γ,
![]()
The ratio between circular sine and cosine is said circular tangent
![]()
By definition we have
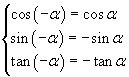
The cosine is an even function, while the sine and the tangent are odd functions, therefore the graph of the cosine is symmetrical with respect to the y axis and the graphs of the sine and the tangent are symmetrical with respect to the origin.
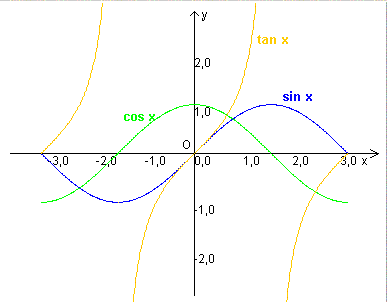
Furthermore, for each integer k,
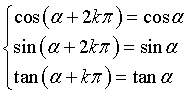
that is, sine, cosine and tangent, are periodic functions with period 2π for the sine and the cosine and π for the tangent.
The following Javascript application allows you to calculate the values of the three functions.
The argument can be expressed as sexagesimal or as real.
If the argument is real it represents radians.
Moreover you can express the argument as a multiple or submultiple of π to be entered as P.
If your browser does not accept the iframe tag, you can directly open its page.
The more P approaches V, the more the circular sector P'OP is indistinguishable from an isosceles triangle having height OV=1 and base PP' = 2 sin α.
In every triangle the ratio between the double of its area and its base is the height. So we can write
![]()
If we move the point P(x;y) counterclockwise around γ sweeping an
angle β, we obtain a new point Q(X;Y) of γ, such that
![]() , where
, where
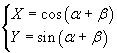
If we apply to the point P(x ; y) of γ the transformation
![]()
we just obtain that
![]() , so
the transformation (1.5) transforms the point P in the point Q.
, so
the transformation (1.5) transforms the point P in the point Q.
In general, the transformations like (1.5) transforms a circumference in itself. These transformations are said rotations.
So we have
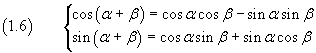
These (1.6) are the addition formulas for the cosine and the sine.
Addition formulas in WolframAlpha.
From these we can easily deduce many other useful identities, like the double-angle formulas
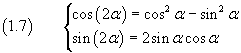
Double-angle formulas in WolframAlpha.
We can also deduce the prosthaphaeresis formulas (or Simpson's formulas)
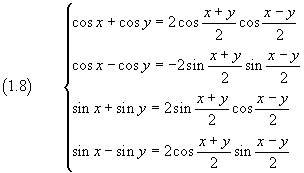
Prosthaphaeresis formulas WolframAlpha
The derivative of sin x with respect to x, by definition, is
![]()
From prosthaphaeresis the numerator is
![]()
so
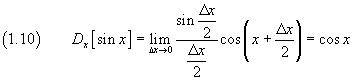
The derivative of cos x with respect to x, by definition, is
![]()
From prosthaphaeresis the numerator is
![]()
so