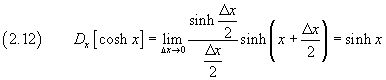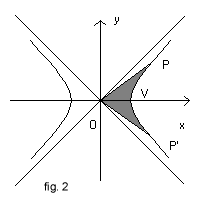

Given in the cartesian plane xOy the graph of the equilateral hyperbola δ
with center in the origin O and unitary real semiaxis, whose equation is
![]() ,
let V be the point where δ intersects the positive semiaxis of abscissas
and P(x;y) any of its points and P' the point of δ symmetrical of
P with respect to the x axis.
,
let V be the point where δ intersects the positive semiaxis of abscissas
and P(x;y) any of its points and P' the point of δ symmetrical of
P with respect to the x axis.
The coordinates x and y of P are functions of the area OPVP'. We can therefore express x and y as parametrical functions of this area α.
These functions are said respectively hyperbolic cosine and sine of α.
So we have
![]()
and, by the equation of δ,
![]()
The ratio between hyperbolic sine and cosine is said hyperbolic tangent
![]()
By definition we have
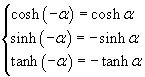
The cosine is an even function, while the sine and the tangent are odd functions, therefore the graph of the cosine is symmetrical with respect to the y axis and the graphs of the sine and the tangent are symmetrical with respect to the origin.
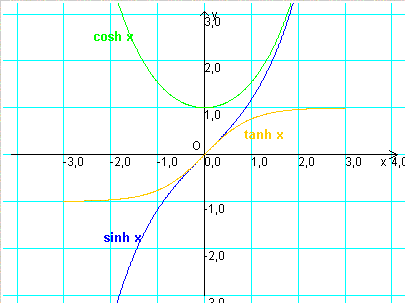
The following Javascript application allows you to calculate the values of the three functions.
If your browser does not accept the iframe tag, you can directly open its page.
The more P approaches V, the more the area OPVP' is indistinguishable from an isosceles triangle having height OV=1 and base PP' = 2 sinh α.
In every triangle the ratio between the double of its area and its base is the height. So we can write
![]()
If we move the point P(x;y) around δ increasing the area α
so that it becomes α+β, we obtain a new point Q(X;Y) of δ,
such that
![]() , where
, where
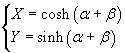
If we apply to the point P(x ; y) of δ the transformation
![]()
we just obtain that
![]() , so
the transformation (2.5) transforms the point P in the point Q.
, so
the transformation (2.5) transforms the point P in the point Q.
In general, the transformations like (2.5) transforms an equilateral hyperbola in itself. These transformations are said hyperbolic rotations.
So we have
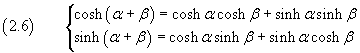
These (2.6) are the addition formulas for the cosine and the sine.
Addition formulas in WolframAlpha.
From these we can easily deduce many other useful identities, like the double-angle formulas
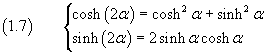
Double-angle formulas in WolframAlpha.
Moreover we can deduce the prosthaphaeresis formulas
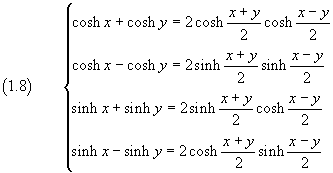
Prosthaphaeresis formulas in WolframAlpha
The derivative of sinh x with respect to x, by definition, is
![]()
From prosthaphaeresis the numerator is
![]()
so
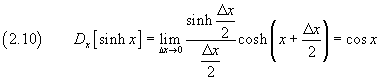
The derivative of cosh x with respect to x, by definition, is
![]()
From prosthaphaeresis the numerator is
![]()
so