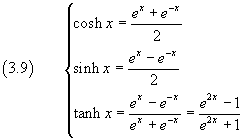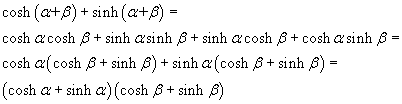
If we sum term by term the addition formulas (2.6) we get
therefore
![]()
If we call exp(x) the sum of the hyperbolic cosine and sine
![]()
from (3.1) we have
![]()
From (3.3) we can deduce that the function exp(x) is a power, because it has a typical property of the powers: the product of two powers of the same base is a power of the same base in which the exponent is the sum of the multiplied powers exponents.
The function exp(x) is said natural exponential and its base
![]()
is usually written e and, sometimes, said the Napier's constant.
The number e is a transcendental irrational whose value, which can be approximated in many ways, is about 2.71828182.
So we can express the function exp(x) as a power of e
![]()
cosh x and sinh x are defined over ℜ, so is their sum ex.
cosh x is always positive and its absolute value is always greater than that of sinh x, so ex is always positive.
If x>0, ex>1, so ex always increases.
In fact, for each positive h,
![]()
Since ex always increases, it has neither maximum nor minimum.
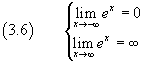
Since the derivative of a sum is the sum of the derivatives of its addends, we have also
![]()
From (3.5) we have
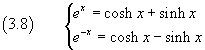
and immediately