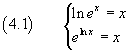
Since the natural exponential function is defined over all ℜ and is always increasing, it is bijective and therefore invertible, that is, it exists a function, that we now call invexp(x), such that invexp(exp(x))=x.
The domain of invexp(x) coincides with the codomain of exp(x), that is, invexp(x) can be applied only to positive real numbers.
The function invexp(x) is commonly said natural logarithm and is denoted by ln (sometimes also by log).
So, by definition,
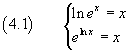
If
then
,
so the equalities
and
are
perfectly equivalent, they represent the same relation between x and y.
In particular, from
we have
and from
we have
.
From the second of (4.1) we have
By applying the derivation chain rule we have
and finally
The equalities
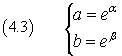
are equivalent to
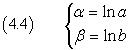
By multiplying term by term the (4.3) we have
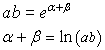
and, from (4.4)
The logarithm of a product equals the sum of the logarithms of its factors.
This property can be immediately extended to any number of factors.
From
we have
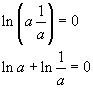
The logarithm of the reciprocal of a number is the opposite of the logarithm of the number itself.
The logarithm of a ratio of two numbers equals the difference between the logarithms of the numbers.
Given
we have
and, raising both the terms to
,
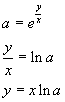
Therefore
The logarithm of a power is equal to the exponent times the logarithm of the base.
The logarithm of a root equals the logarithm of the radicand divided by the index of the root.