From (4.8) ln ax =x ln a, we have
![]()
Exponential functions ax, with base a other than e, equal a natural exponential function in which the exponent x is multiplied by the natural logarithm of the base a.
However, since ln a is a real function only if a>0, such functions are real only if a>0. Since 1x=1 for whatever x, if a=1 the exponential cannot be inverted. Otherwise, these functions inherit the same properties of the natural exponential: they are always positive and monotonic (increasing if a>1, decreasing if a<1), so they are invertible.
The following Javascript application allows you to tabulate and graph exponential functions with real base.
The natural base can be entered in the input fields as E (uppercase).
If your browser does not allow internal frames, you can directly access the application page.
The browser must allow pop-up windows.
The inverse functions of each of these exponential functions is said logarithm to base a and is denoted by loga.
The logarithm to base 10, said common logarithm, are often denoted by Log.
By definition
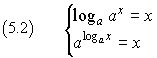
From the second one of the (5.2) we have
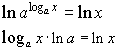
![]()
The logarithm to base a of a real number x is directly proportional to the natural logarithm of x; it equals the ratio between this natural logarithm and the logarithm of a.
Since the logarithm to base a is proportional to natural logarithm, it inherits all its algebraic properties. For example:
![]()
that is
whatever the base, the logarithm of a product equals the sum of the logarithms of its factors.
The following Javascript application allows you to tabulate and graph logarithmic functions with real base.
The natural base can be entered in the input fields as E (uppercase).
If your browser does not allow internal frames, you can directly access the application page.
The browser must allow pop-up windows.