The function
![]()
isn't defined at x=0, but this singularity is removable because the limit as x→0 is finite, as we can easily see by applying De L'H˘pital's rule. The same thing is true for its derivatives:
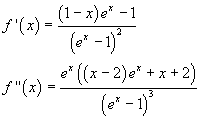
We can therefore expand this function using the MacLaurin series expansion
![]()
where Bn is the limit as x→0 of the n-th derivative of f(x):
![]()
In this way we can find:
![]()
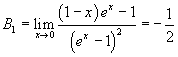
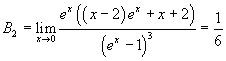
and so on. The Bn are said Bernoulli numbers, from the name of the mathematician who first used them in his Ars conjectandi, a treatise on probability theory.
The calculation of the derivatives and of their limits, even using powerful software, is slow and does'nt give any hints to conjecture a general relation between the numbers Bn which could allow a more direct algorithm to generate these numbers. Such algorithm can be found using the well known series expansion of the natural exponential function in the following way.
From
![]() we have
we have
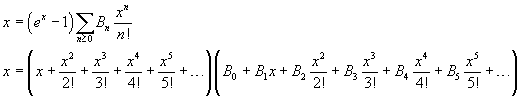
Now we multiplicate all the addends in the second sum by every addend of the first
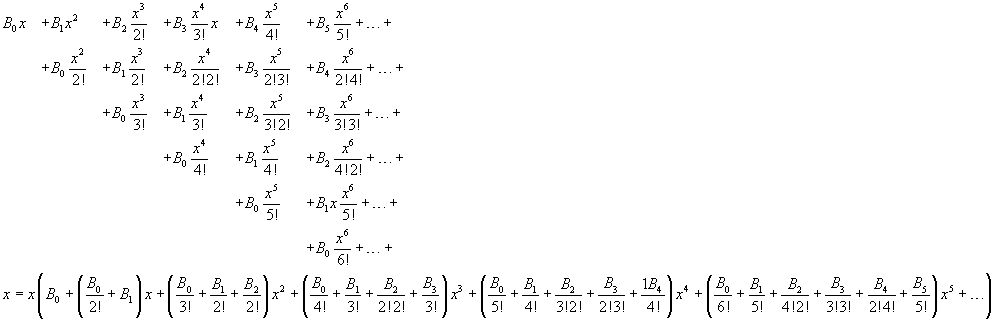
The first and the second term are identical only if, in the second term, B0=1 and the sum of the coefficients of the same power of x is 0. So
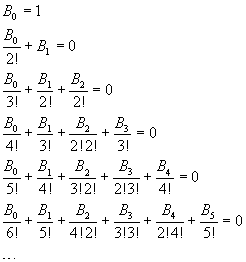
The denominators in these sums coincide with the denominators of the factorial expansions of the binomial coefficients.
![]()
Using the binomial coefficients, we can write the n-th calculated row as
![]()
If we consider, for example, the last calculated row, we have
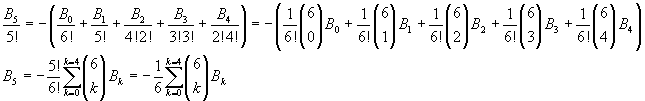
So, in general, we can write
![]()
This allows the recursive calculation of every Bn
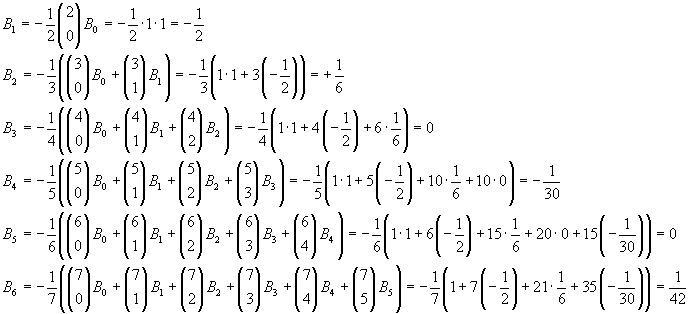
To obtain further Bn, we may automatize the calculation
as in the following Javascript application.
If your browser does not allow the iframe tag, you can open the source page.
From the explicitly calculated values and using the applet, we can conjecture that all the Barnoulli's numbers with odd index ≥ 3 are null. This is true, because from
![]()
we have
![]()
and after
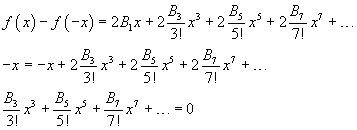
So, every B in the first term must be 0.
Given the function
![]()
let En be the values taken by it and its successive derivatives for x=0. The values En are said Euler's numbers. If we expand this function in Maclaurin series, we have
![]()
and then
![]()
If we explicitly represent some of the summands of the factors in the right-hand side, we obtain
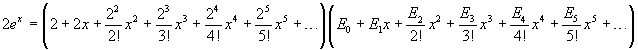
The expansion of this product is
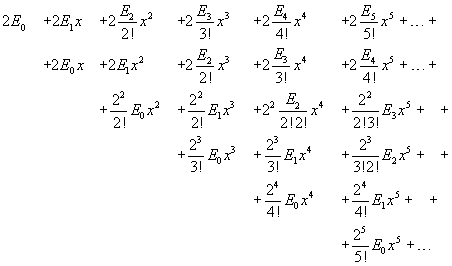
then
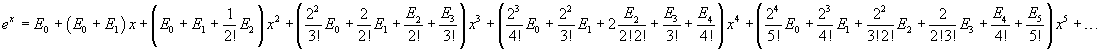
Two polynomials in the same variable are identical only if the same powers of the variable have equal coefficients, so the coefficients of powers of x in the right-hand side must coincide with the coefficients of the series expansion of the exponential. These identities allow us to calculate recursively the values of En. Infact
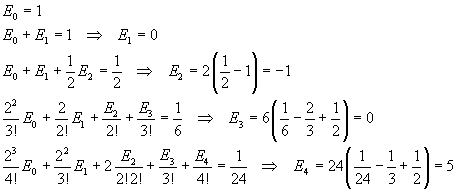
Obviously E5, like E1 and E3, is 0, because all En with odd n are null, since s(x) is an even function. The identity between the coefficients of the fifth power can be useful in conjecturing a general calculation method.
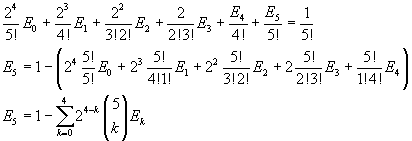
We can conjecture that, in general,
![]()
To obtain further En, we may automatize the calculation
as in the following Javascript application.
If your browser does not allow the iframe tag, you can open the source page.
There are different conventions on the notation of Euler numbers. Here we assume the convention adopted by Mathematica
for the function EulerE[n].