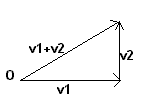
If a car, starting from the point O, first moves 4km toward E and after moves 3km toward N, its final distance from O is 5km and the direction of the displacement is halfway between E and N.
The final displacement from O can be considered the sum ot the two successive displacements and obviously it isn't the arithmetic sum of their lengths. If we draw the vectors representing the two successive displacements, the final position of the car is well represented by a vector which has the tail in O and the head coincident with the head of the second displacement.

We reach the same result if we apply both the initial vectors to the point O and draw the diagonal from O of the parallelogram formed by them.
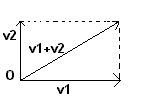
In general the sum of any two vectors is made in the same way.
It is easy to verify that the sum of two vectors is independent from the order of the addends: it is commutative.
If two vectors are parallel, have same magnitude but opposite direction, their sum has magnitude 0, so it is impossible to know its direction. Nevertheless we'll consider also such sum as a vector and we'll call it a null vector.
Obviously, the sum between any vector and the null vector gives the first vector, so the null vector is the neutral (or identity) element of the sum.
When the sum of two vectors is null, the vectors are said opposite.
Given three vectors,
we'll obtain the same vector.
This property of the vector sum, like the analogous property of the sum of real numbers, is said associative property.
The set of the geometric vectors with vector sum on it is therefore an abelian group.
In a group we can define the inverse operation: in this case the vector difference: the vector difference between two vector is done by the sum between the first vector and the opposite of the second vector.
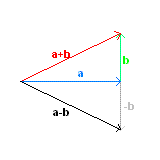
Since translated vectors are equivalent, the difference vector can be obtained applying both the vectors to O and drawing a vector from the head of the subtrahend to the head of the minuend.