A vector admits multiples and submultiples.
Given the vector v, its m-nth multiple w is the sum of m vectors each equal to v; we can write w = mv;
conversely, there exists a vector u such that v = nu;
u is the n-nth submultiple of v and we can write
Multiples and submultiples of v have the same direction as v.
y, the m-nth multiple of u can be written as
;
it too has the same direction as v but its length is
with respect to that of v.
Therefore we can define the product of a rational number times a vector and, more generally, the product of a real number times a vector; in this context, the real number is said a scalar.
Scalar times a vector is a vector with same direction as the multiplicand vector and magnitude equal to its magnitude times the scalar.
If we note
the magnitude of v, we have that
is a vector with the same direction as v and magnitude = 1.
When a vector has magnitude=1, it is said a unit vector; often unit vectors are
called versors.
The unit vector
is
therefore said the versor of v.
Given two vectors a and b applied to the same point O, let α be their plane. If the the least rotation required to superimpose a to b is counterclockwise, we can represent such rotation as a versor perpendicular to α and oriented from α to the observer: this is the rotation versor.
If the rotation is clockwise, the rotation versor is opposite to the former.
Two vectors a and b applied to the same point O determine a parallelogram with sides equal to the magnitudes of the vectors. If we multiply the rotation versor of a and b by the area of this parallelogram, we obtain a vector c said the cross product of a and b.
The cross product c is written as
and sometimes as
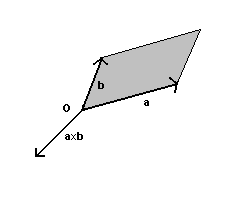
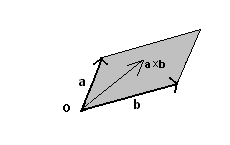
The cross product is not commutative. If we change the vectors' order we obtain the opposite vector:
The cross product of parallel vectors is null.
In particular, the cross product of a vector by itself is null.
The magnitude of the cross product of two given vectors has a maximum when the vectors are perpendicular.
The area of a parallelogram coincides with the area of a rectangle with equal base and equal altitude. If we know the lengths a and b of its sides and an angle θ between them and let a be the base, the altitude of the rectangle must be b sin θ. The magnitude of the cross product is therefore
We can also associate to two given vectors a and b, applied to the same point O, the area of the rectangle in which a side has length given by the magnitude of either vector, say a, and the other side has length equal to that of the projection of the second vector, say b, on the line of action of the first vector. Furthermore, we can consider this area as negative if the projection lies outside the first vector, positive (or eventually null) otherwise.
The real number so obtained is said the dot product of a and b.
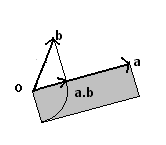
It must be emphasized that the dot product is not a vector, but a real number.
The dot product is commutative.
If two vectors are perpendicular, their dot product is null.
Given two vectors, the magnitude of their dot product has a maximum when they are parallel.
The square of a vector is given by the square of its magnitude.
If we know the magnitudes of a and b and the angle θ between them, the length of the projection of b on the line of action of a is given by b cosθ, so the dot product is
