Language and syntax of Mathematica

Documentation about the Mathematica language

if you want to set up mathematical calculations in a typewritten line, the more clearly, safe and fast, not to have the answer Wolfram | Alpha does not understand your query, that you have is to use the native language and syntax of Mathematica adopted from the first releases. Wolfram provides extensive documentation at he page Wolfram Mathematica 8 Documentation.

On this page you have to write, in the SEARCH field, what you want, for example, solution of an equation, and then you must click the button with the quotes >> and follow the links until you reach the desired documentation page Solve that, in addition to informing about the syntax, presents numerous examples and links to related pages.

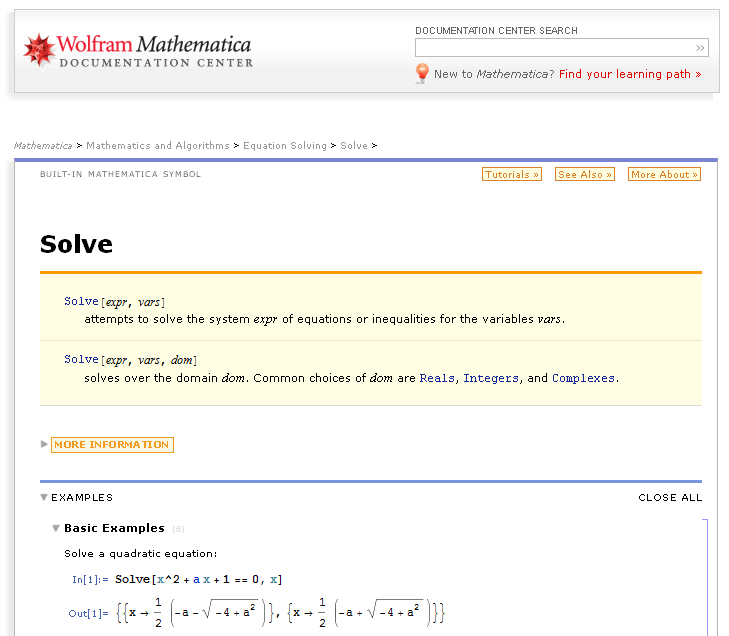
If you know the name of the operator you search, but want documentation on its syntax, you can start searching directly from the documentation, in alphabetical order, of the numerous functions implemented, which can be found on page Alphabetical Listing - Wolfram Mathematica 8 Documentation.

For example, if by the latter page you click Solve, you arrive to the same page.

Following the instructions in this documentation, you can ask for the solution of a general equation of the second degree:

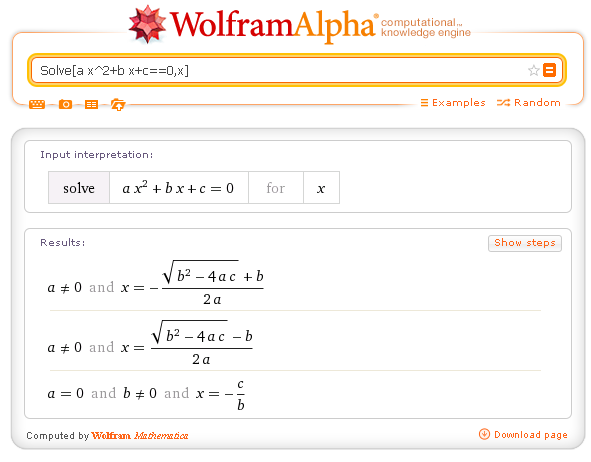
However, even using the language of Mathematica, the calculation can not be executed because WolframAlpha, at least in the free version, does not fully support all functions of Mathematica.

Orthographic rules

• The expressions must be written using the alphanumeric characters of ASCII, ie those present in the keyboard
• The decimal separator must be a period.
• The sign of multiplication is the asterisk *, which is optional, but if you leave out the asterisk, you will need to remember to insert a space between the factors, because, of course, if two symbols are joined, they form a single symbol.
• The sign of division is the right slash /.
• The sign of exponentiation is the caret ^.
• The order of operations is indicated by parentheses (), possibly nested and always well balanced.
• In the absence of parentheses, the normal rules of precedence are applied.
• Square brackets are used only to contain the arguments of functions or operators; they are required.
• The libraries of Mathematica provide a great amount of predefined numeric values, functions and operators that can be immediately used; all entities (numbers, functions, operators) have the first letter capitalized and their arguments must be delimited by square brackets. In particular, real transcendental numbers greek pi π and the natural basis e (Euler's number) must be written respectively as Pi and E. The imaginary unit is written I.
• In general, Mathematica assumes that the variables are complex numbers. It is possible, for example, calculate the solutions of x²+x+1=0 or the arcsine of 2.
• The real arguments of the circular functions are expressed in radians.
• If it is possible, Mathematica calculates mathematically exact results. Otherwise shows decimal approximations.
• Mathematica can also operate on lists of objects (for example, representing vectors or arrays). Lists are comprised between braces and their elements are separated by commas.