The operator Solve allows to solve equations and systems. Solve requires two arguments: an equation (or a list of equations to represent a system) and a variable (or list of variables in the case of a system).
The equals sign in Mathematica is given (as in Javascript, C and Java) doubling the usual sign.
Examples.
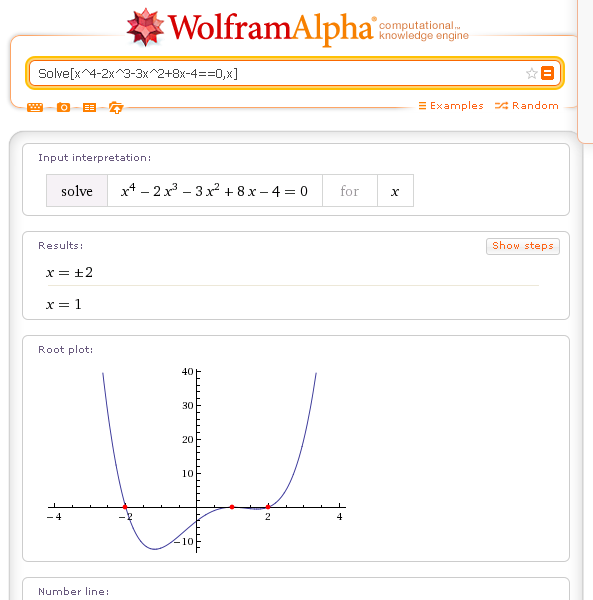
Algebraic equation: Solve[x^4-2x^3-3x^2+8x-4==0,x]

Trigonometric equation: Solve[Cos[x]==Sqrt[3]/2,x]
WolframAlpha: Trigonometric equation
System: Solve[{x+y==3,x-y==1},{x,y}]
Algebraic equation: Solve[6x^3-13a x^2+9a^2 x-2a^3==0,x]
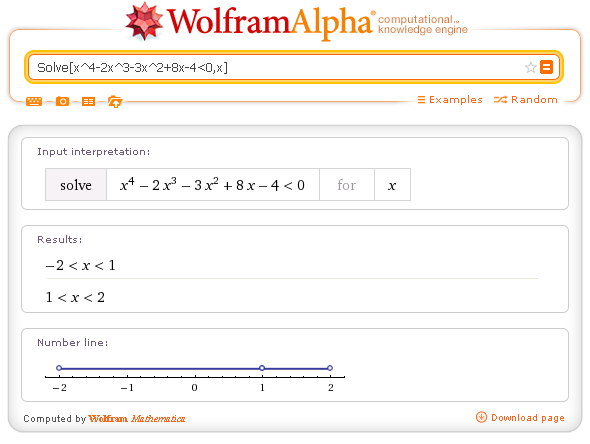
The operator Solve allows also to solve inequalities in one or more variables.
Example.
Algebraic inequality: Solve[x^4-2x^3-3x^2+8x-4<0,x]