(note a cura di Roberto Bigoni)

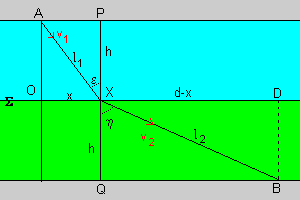
Una particella puntiforme si muove attraversando due strati contigui di ugual spessore h, rappresentati in azzurro e in verde nella figura. La particella entra nello strato azzurro nel punto A, attraversa la superficie Σ di separazione tra i due strati nel punto X ed esce dallo strato verde nel punto B. Nello strato azzurro ha velocità costante di intensità v1; nello strato verde ha velocità pure costante di intensità v2. Si assume che le due velocità siano complanari.
Per determinare la traiettoria AXB di durata minima si può procedere nel seguente modo.
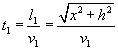
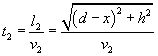
La durata totale t del percorso risulta quindi
(1.1)
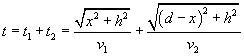
La derivata di t rispetto a x è
![]() e si annulla se
e si annulla se
(1.2)
![]()
dove ε e η sono gli angoli che i due segmenti di traiettoria formano con la perpendicolare alla superficie Σ in S e k è il valore costante del rapporto tra velocità e seno.
Quindi condizione necessaria perché la traiettoria abbia durata minima è che il seno dell'angolo che un segmento di percorso in uno strato forma con la perpendicolare alla superficie di separazione con un altro strato sia direttamente proporzionale al modulo della velocità nello strato stesso.
Dalla (1.2) si deduce la proporzionalità tra i seni
![]() .
.
Questo è il comportamento della luce che si propaga in due mezzi ottici contigui in cui essa ha diversa velocità. Il fenomeno del cambiamento della direzione di un raggio luminoso è detto rifrazione. La costante n21 è detto indice di rifrazione relativo del secondo strato rispetto al primo.
La legge della rifrazione, forse già rilevata dall'arabo Ibn Sahl attorno all'anno 1000, è stata riosservata nel Seicento da W. Snell e da Cartesio ed è nota come legge di Snell (in Francia come Legge di Descartes).
Va però osservato che, matematicamente, l'annullamento della derivata è condizione necessaria ma non sufficiente: l'annullamento della derivata prima può comportare anche un massimo o un flesso orizzontale (saddle=sella in inglese). In generale si può quindi dire che l'annullamento della derivata è condizione necessaria e sufficiente per una situazione stazionaria.
In ottica si può quindi affermare che, se un raggio di luce si propaga da un punto A ad un punto B esso segue il percorso che rende stazionaria la durata della traiettoria.
Questa stessa legge fu formulata, sempre nel Seicento, da P. Fermat.
Se un raggio di luce attraversa consecutivamente n mezzi diversi percorrendo in ognuno di essi un tratto li con velocità vi, la durata del percorso totale risulta
![]()
Il rapporto tra velocità c della luce nel vuoto e la velocità v della luce in un mezzo ottico è detto indice di rifrazione assoluto n del mezzo. Si può quindi scrivere
![]()
Ovviamente, se un percorso minimizza t, minimizza anche la somma
![]()
detta lunghezza del cammino ottico. Se l'indice di rifrazione varia con continuità, la somma va sostituita da un integrale:
![]()
La γ sotto il segno di integrale rappresenta la traiettoria percorsa dal raggio. Si può quindi enunciare il principio di Fermat nel seguente modo: Un raggio di luce si propaga da un punto A ad un punto B seguendo un percorso corrispondente ad un cammino ottico di lunghezza stazionaria.
In questa forma, la legge è più generale della legge di Snell perché oltre che alla rifrazione, può applicarsi anche alla riflessione.
Una particella in un campo gravitazionale costante di intensità costante g si muove variando continuamente l'intensità della sua velocità v in funzione della sua quota y secondo una relazione che può essere dedotta dal principio di conservazione dell'energia.
![]()
In particolare, se una particella si trova inizialmente ferma nell'origine O di un sistema
di riferimento cartesiano ortogonale Oxy,
![]() e quindi
e quindi
(3.1)
![]()
Analogamente a quanto succede per i raggi luminosi, dovrà esistere anche per le particelle una traiettoria di durata minima, detta brachistocrona (dal greco brachystos='brevissimo' chronos='tempo'; la corretta grafia inglese dell'aggettivo è quindi etimologicamente brachystochrone).
La determinazione della traiettoria brachistocrona, già tentata da Galileo, che ipotizzò erratamente che fosse un arco di circonferenza, appassionò gli scienziati europei tra Seicento e Settecento con lo sviluppo di metodi di calcolo sempre più raffinati e generali, può tuttavia essere ottenuta in modo abbastanza diretto.
Dalle (1.2) e (3.1) si ha
![]()
(3.2)
![]()
Il minimo valore -h dell'ordinata y si ha nel punto V per cui sin θ = 1.
La traiettoria più veloce può essere determinata nel seguente modo.
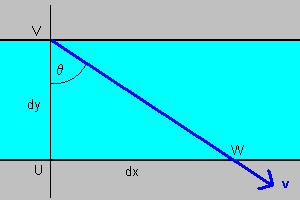
Si considera un generico strato orizzontale di spessore dy, si indica con v l'intensità della velocità della particella in tale spessore, con θ l'angolo che la velocità forma con la verticale, con -h la quota minima.
![]()
![]()
Derivando y rispetto a θ
(3.3.1)
![]()
Osservando poi che
![]()
si ottiene anche
(3.3.2)
![]()
In definitiva, unendo la (3.3.1) e la (3.3.2),
(3.4)
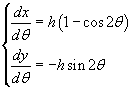
Integrando queste equazioni si ottengono le espressioni parametriche delle coordinate in funzione di θ
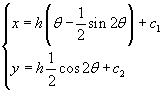
In O, θ, x e y sono nulli, condizione che permette la determinazione di c1 e c2.
(3.5)
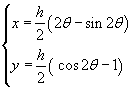
Le (3.5) descrivono una curva passante per l'origine O, per il punto S(hπ ; 0), simmetrica rispetto alla retta verticale passante per il punto V (vertice) in cui ha un minimo assoluto.
Tale curva è detta cicloide. Graficando le (3.5) per θ da 0 a π, ad esempio per h=2 con Mathematica (©Wolfram), si ottiene
ParametricPlot[{2 t-Sin[2t],Cos[2t]-1},{t,0,Pi},AspectRatio→1,PlotRange→{-2Pi,0}, PlotStyle→{RGBColor[1,0,0]}]
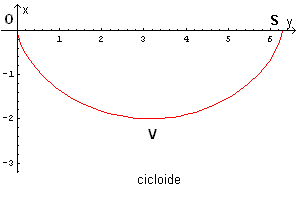
La cicloide descrive la traiettoria di un punto di una circonferenza che rotola su un piano.
Dalle (3.4) si ricava
(5.1)
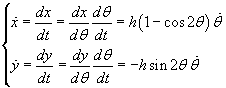
Le (5.1) esprimono le componenti cartesiane della velocità: la somma dei loro quadrati è il quadrato della velocità v:
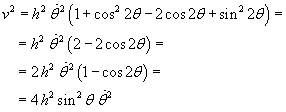
![]()
La derivata di θ rispetto al tempo è costante, dunque θ è funzione lineare del tempo e, dato che θ è inizialmente nulla,
(5.2)
![]()
Sostituendo questa espressione di θ nelle (3.5) si ottengono le equazioni orarie del moto:
(5.3)
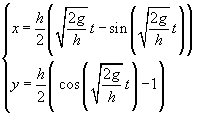
Dalla (5.2) si deduce il tempo T necessario per scendere dal punto O al punto V di ordinata minima -h:
![]()
(5.4)
![]()
Una particella che, partendo da ferma, scivolasse senza attriti su un piano inclinato da O a V in virtù del suo peso, impiegherebbe un tempo Ti maggiore di T.
Dalla prima delle (3.5) l'ascissa del punto V risulta
![]()
La lunghezza del piano inclinato è quindi
![]()
Indicando con δ l'angolo di inclinazione del piano rispetto all'orizzontale, la componente γ dell'accelerazione di gravità parallela al piano risulta
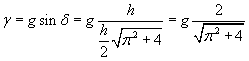
Da ![]() si ricava
si ricava
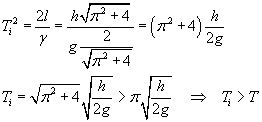
Le analisi precedenti acquistano interesse operativo solo se, dato un punto qualunque P(α ; -β) (α e β positive) si riesce a determinare l'equazione della cicloide passante per tale punto, cioè il valore da assegnare al parametro h nelle (3.5).
A questo scopo si può procedere come segue.
Dalla seconda delle (3.5) si calcola θ in funzione di y:
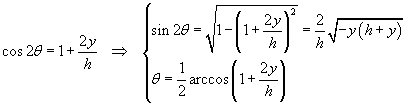
Dalla prima delle (3.5) si ottiene
![]()
Sostituendo a x e y le coordinate di P si ottiene l'equazione in h
(6.1)
![]()
La soluzione della (6.1) va approssimata con un metodo numerico.
Ottenuta una valutazione di h, dalla prima delle (3.5) si ottiene un'equazione che permette di valutare il valore del parametro θ corrispondente all'ascissa del punto d'arrivo P.
![]()
Infine, dalla (5.2) si ottiene la durata della discesa al punto P:
![]()
La seguente applicazione premette di calcolare e rappresentare la traiettoria brachistocrona dall'origine O ad un punto predeterminato P, calcolando il tempo di discesa sulla brachistocrona e confrontandolo con il tempo che sarebbe necessario per effettuare la stessa discesa lungo un piano inclinato. Mostra il fatto controintuitivo che, sebbene la lunghezza dell'arco di brachistocrona sia maggiore del segmento di piano inclinato, la durata della traiettoria brachistocrona è minore. L'unità di misura per ascissa e ordinata è il metro. Non esagerare con valori troppo grandi per le possibilità grafiche dell'applicazione.
ultima revisione: Maggio 2018