Misura del rapporto
tra i calori specifici molari (γ) dell'aria
(Metodo di Clément-Desormes)

(note a cura di Roberto Bigoni)

English version

1. Introduzione.

Nello studio della teoria cinetica dei gas perfetti si è dedotta la Legge di Poisson per le trasformazioni adiabatiche che afferma che in una trasformazione adiabatica da uno stato iniziale A ad uno stato finale B vale la relazione

dove P e V sono la pressione e il volume e γ è il rapporto tra calore specifico a pressione costante (c_p) e il calore specifico a volume costante (c_v).

La teoria cinetica dei gas perfetti deduce anche precisi valori per γ

• γ = 5/3 per il gas monoatomici
• γ = 7/5 per un gas biatomico
• γ = 4/3 per un gas poliatomico

Per sottoporre la teoria cinetica dei gas perfetti ad un controllo cruciale si potrebbe cercare di misurare sperimentalmente il valore di γ per un gas reale a molecole monoatomiche (elio, neon,...), biatomiche (ossigeno, azoto, idrogeno...) o poliatomiche (anidride carbonica, ammoniaca, metano...) per vedere se i risultati non disconfermino le previsioni teoriche.
Non disponendo di attrezzature specializzate, ci si può limitare a tentare di misurare il γ dell’aria atmosferica, con l’avvertenza di ricordare che essa non è un gas omogeneo ma è una miscela di azoto e ossigeno con tracce significative di altri gas.
Data comunque la prevalenza in essa di molecole biatomiche di azoto e ossigeno, il valore da ottenere non si dovrebbe discostare troppo da 1.4.

2. Metodo di misura.

Per riuscire a misurare il γ di un gas bisogna ottenere una sua espressione in funzione di grandezze sperimentalmente misurabili. Tali grandezze non possono essere c_p e c_v che non sono facilmente osservabili, ma altre grandezze più facilmente accessibili, come, ad esempio, le pressioni.

Questa via viene seguita nel metodo messo a punto da Clément e Desormes.

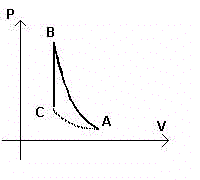
Al gas contenuto in un recipiente si fa subire una compressione adiabatica che dallo stato A(P_A,V_A,T_A) lo porta nello stato B(P_B,V_B,T_B). La temperatura T_B sarà maggiore di T_A.

Dalla legge di Poisson (1) si ricava

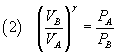
Dalla legge generale dei gas perfetti

si ricavano

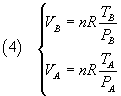
Dividendo le (4) membro a membro si ottiene

Sostituendo nella (2) il secondo membro della (5)

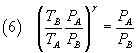
Se ora dallo stato B si passa allo stato C(P_C,V_C,T_A), dove la temperatura ritorna a T_A con un raffreddamento isocoro, per la legge di Gay-Lussac si ha

cioè

E, sostituendo nella (6) e quindi semplificando, si ottiene

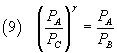
Per risolvere questa equazione rispetto a γ si calcola il logaritmo di entrambi i membri ottenendo

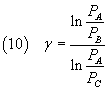
Si riesce così ad esprimere γ in funzione delle pressioni dei tre stati ai quali è stato portato il gas: misurando tali pressioni si può quindi calcolare γ.

Per misurare le pressioni ci si può servire di un barometro a liquido di densità ρ.
Se si organizza la misura in modo che P_B coincida con la pressione atmosferica ambiente P₀ (~ 1 Atmosfera), le pressioni P_A e P_C possono essere espresse con la legge di Stevin

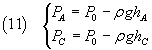
Il numeratore della (10) può essere scritto

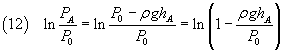
Dato che, per piccoli valori di x , ln(1-x) ~ -x, il numeratore della (10) può essere approssimato in

Il denominatore della (10) può essere scritto

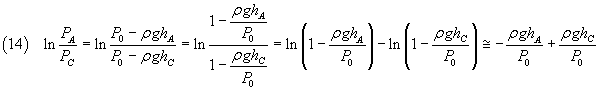
In definitiva la (10) è ben approssimata dalla

3. Laboratorio.

Per potere utilizzare la (15) per la misura del γ dell’aria è necessario far compiere ad una massa d’aria, inizialmente nello stato A(P_A,V_A,T_A) una trasformazione adiabatica che la porti nello stato B(P_O,V_B,T_B) e quindi una trasformazione isocora che la porti nello stato C(P_C,V_C,T_A) potendo, nei tre stati, misurare le pressioni con le altezze di un liquido barometrico.

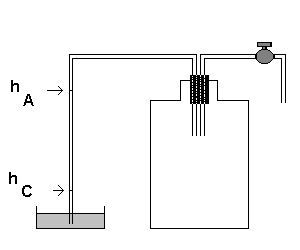
Un modo per realizzare questa situazione sperimentale è il seguente.

1. Si chiude una bottiglia di vetro del volume di circa 5 litri con un tappo a tenuta e si fanno passare nel tappo due tubi.
   Un tubo è collegato ad un manometro a liquido, nel quale l’altezza del liquido è proporzionale alla differenza tra la pressione dell’aria atmosferica e la pressione dell’aria nella bottiglia.
   L’altro tubo, munito di una chiavetta per aprire e chiudere i flussi d’aria, è collegato inizialmente a una pompa aspirante (realizzabile con un tubo di Venturi) e successivamente con l’ambiente esterno.
   In condizione di riposo, nella bottiglia l’aria è a pressione atmosferica P_O e a temperatura ambiente T_A.
2. Per portare l’aria della bottiglia nello stato A si attiva la pompa che, estraendo parte dell’aria interna produce nella bottiglia una depressione. Si aspira fino a che il liquido barometrico riempie il tubo barometrico (evitare di prolungare oltre l’aspirazione, perché il liquido finirebbe nella bottiglia).
3. Questa aspirazione produce una espansione adiabatica dell’aria interna ed un suo conseguente raffreddamento a temperatura inferiore a quella ambiente.
4. Terminata l’aspirazione si attendono alcuni secondi e si osserva che il livello del liquido cala rispetto al massimo raggiunto nell’aspirazione.
   Questo fatto si spiega con il flusso di calore dall’ambiente (caldo) all’interno (raffreddato) che continua fino all’equilibrio termico tra interno ed esterno.
   L’aria interna si riscalda aumentando la propria pressione, che rimane comunque inferiore a quella esterna.
5. Ora l’aria interna è nello stato A nel quale la temperatura è la temperatura ambiente T_A e la pressione P_A, inferiore a quella ambiente, è misurabile dall’altezza h_A del liquido nel barometro.
6. Si misura h_A con una riga millimetrata.
7. Per realizzare la trasformazione adiabatica AB, staccato il secondo tubo dalla pompa, si apre la chiavetta e poiché le pressione esterna è maggiore di quella interna c’è un flusso d’aria dall’esterno all’interno, segnalato da un fruscìo nella chiavetta.
   Il fruscìo cessa quando la pressione interna eguaglia quella esterna. Appena il fruscìo cessa, con mossa precisa e decisa (è l’operazione più delicata di tutta la misura) bisogna chiudere la chiavetta, isolando l’interno dall’esterno.
   In questa operazione l’aria interna, prima a bassa pressione P_A, viene compressa fino alla pressione ambiente P_O.
   Se l’operazione è veloce, questa compressione è adiabatica perché il flusso di calore tra interno ed esterno è trascurabile. La compressione adiabatica riscalda l’aria interna.
8. Ora l’aria interna è nello stato B.
   La pressione interna è uguale a quella esterna P_O, ma la temperatura T_B è superiore a quella esterna.
9. Attendendo ancora alcuni secondi si osserva un innalzamento del liquido nel barometro. Ciò è dovuto al fatto che essendo la temperatura interna maggiore di quella esterna, c’è flusso di calore dall’interno verso l’esterno che dura fino al ristabilimento dell’equilibrio termico tra i due ambienti, cioè fino a che la temperatura interna non ritorna uguale a T_A.
   Questa è la trasformazione BC che, a chiavetta chiusa, può essere considerata isocora, data la trascurabile variazione di volume interno dovuta alla risalita del liquido.
10. Quando l’altezza del liquido si stabilizza, l’aria interna è nello stato C, con temperatura uguale a quella iniziale T_A e pressione P_C, inferiore a quella atmosferica, rilevabile dall’altezza h_C del liquido barometrico.
11. Si misura h_C con una riga millimetrata.

Si hanno quindi le misure h_A e h_C necessarie per ricavare γ dalla (15).

Poiché la tecnica di misura fa affidamento sull'abilità manuale dello sperimentatore, le misure saranno inevitabilmente soggette ad errori casuali: per una buona misura e per una buona valutazione dell'incertezza su di essa bisognerà replicare più volte la misura stessa ed associarle come incertezza il triplo della deviazione standard.

Il lavoro di una studentessa

ultimo aggiornamento: Giungo 2020