5. Definizioni - Identità

1. definizioni

   • Vettore gradiente di un campo scalare φ: prodotto algebrico di per φ: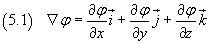

     

   • Scalare divergenza di un campo vettoriale h: prodotto scalare di per h: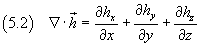

     

   • Vettore rotore di un campo vettoriale h: prodotto vettoriale di per h:

     

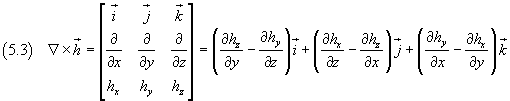
2. identità

   • Rotore del gradiente di un campo scalare φ: è nullo:

     

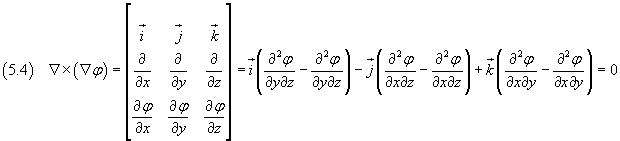
   • Divergenza del rotore di un campo vettoriale h: è nulla:

     

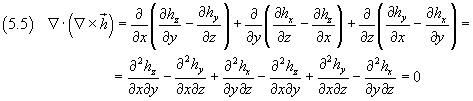
   • Divergenza del gradiente di un campo scalare φ: è la somma delle derivate parziali seconde di φ.

     Tale somma è detta laplaciano dello scalare φ ed è spesso indicata dal simbolo Δ (oppure ).

     

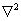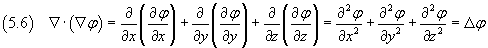
   • Gradiente della divergenza di un campo vettoriale h:

     

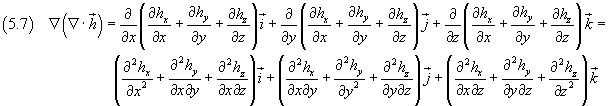
   • Rotore del rotore di un campo vettoriale h:

     

     

     

     

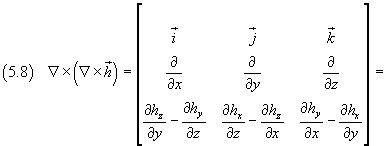
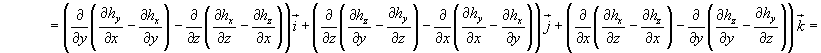
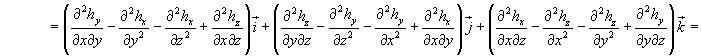
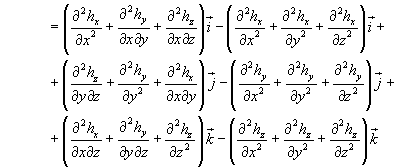
     Introducendo il simbolo del laplaciano di un vettore

     

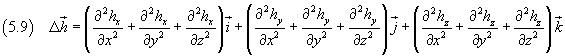
     Dalla (5.6) si ottiene con notazione più concisa

     

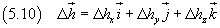
     Infine, utilizzando l'identità (5.7), si conclude che il rotore del rotore è uguale al gradiente della divergenza meno il laplaciano: