Se un punto del mezzo che supporta un'onda è vincolato all'immobilità la sua energia è forzatamente nulla e quindi attraverso di esso non può fluire energia: questo punto costituisce una barriera che impedisce all'onda di oltrepassarlo.
Per semplificare le comprensione del fenomeno si può considerare un'onda unidimensionale come, ad esempio, quelle che si propagano sulle corde degli strumenti musicali. In queste corde, che in questo caso costituiscono il mezzo di propagazione dell'energia, gli estremi sono vincolati, fissati allo strumento, e quindi non possono vibrare come gli altri punti della corda: la loro energia è costantemente nulla e quindi attraverso di essi non può fluire energia.
Come succederebbe ad una particella che colpisce una parete rigida con velocità perpendicolare alla parete stessa, l'onda inverte la propria velocità e si propaga in direzione opposta a quella di provenienza fino ad incontrare l'altra barriera dalla quale viene nuovamente riflessa e così via.
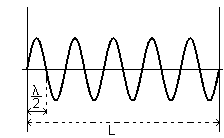
Onde progressive e onde regressive interferiscono mutuamente producendo come risultato un'onda vincolata ad avere nodi agli estremi della corda. Questa condizione implica che la lunghezza del mezzo deve contenere esattamente un numero intero di semilunghezze d'onda.
Detta L la lunghezza del mezzo e λ la lunghezza d'onda
Se il mezzo è sede di un'onda stazionaria, tutti i suoi punti si comportano come oscillatori armonici di uguale pulsazione ω ma di ampiezza variabile a seconda della loro distanza da uno degli estremi. Ponendo 0 la posizione di un estremo e L la posizione dell'altro, con una opportuna scelta dell'istante iniziale, lo stato del mezzo al tempo t è descritto dall'equazione
nella quale l'ampiezza C sin kx si deve annullare quando x è un multiplo della semilunghezza d'onda, in particolare quando x è uguale a una semilunghezza d'onda:
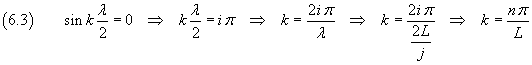
Si ha quindi
Si può assumere la (6.4) come l'equazione della n-esima funzione d'onda stazionaria su un mezzo unidimensionale di lunghezza L con nodi sugli estremi.
animazione
La costante C dipende dall'energia totale
residente nel mezzo.
Indicando con μ la densità lineare del mezzo unidimensionale
l'energia di una masserella dm oscillante con pulsazione ω e ampiezza A risulta, per la (3.9)
Nella (6.4) l'ampiezza è 
, quindi
La somma delle energie di tutte le masserelle dm estesa al tutto il mezzo è l'energia totale residente nel mezzo
Si ottiene quindi
Il valore di C così ottenuto, inserito nella (6.5), produce
e quindi
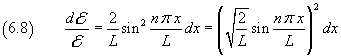
La (6.8) mostra che la frazione dell'energia totale compresa tra x e x+dx è proporzionale al quadrato di
cioè che la densità dell'energia nella posizione x è tanto maggiore quanto maggiore è il quadrato di ψn.
Il quadrato di ψn rappresenta quindi la funzione di distribuzione della densità di energia lungo l'asse x.
La (6.9) è indipendente da μ, quindi vale non solo per un'onda materiale, ma per un'onda qualunque.
Allora assumendo
e sostituendo nella (6.4)
si ottiene l'equazione dell'ennesima equazione d'onda stazionaria che può sussistere in un mezzo unidimensionale di lunghezza L normalizzata in modo che il quadrato dell'ampiezza rappresenti la densità relativa di energia.
La stessa funzione d'onda (6.11) può più sinteticamente essere scritta
con
Se nello stesso mezzo si sovrappongono più onde stazionarie, supposte tutte vincolate ad avere nodi alle estremità del mezzo stesso, l'interferenza tra queste onde, in questo caso dette armoniche, produce configurazioni d'onda piuttosto complicate. Questo è ciò che avviene, ad esempio nelle parti vibranti degli strumenti musicali che sono sede della sovrapposizione di più armoniche che caratterizzano il timbro del suono emesso.
animazione
Se si interpreta la densità di energia come densità di probabilità di presenza di energia in una determinata posizione, l'equazione (6.13) rappresenta la certezza del fatto che tutta l'energia del sistema è situata nell'intervallo [0 ; L].
Fissando all'interno di questo intervallo le posizioni x1 e x2, l'integrale
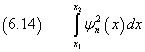
rappresenta la probabilità che ci sia energia nell'intervallo Δx = [x1 ; x2].
Se si considera un sistema formato da un grande numero di armoniche interferenti, si osserva che questa probabilità tende a 0 tranne che in un ristretto intervallo in cui appare concentrata la totalità dell'energia. Se il numero delle armoniche tende all'infinito, l'ampiezza di questo intervallo tende a 0.
Questo intervallo non è statico, ma si muove con velocità costante rimbalzando contro le pareti proprio come farebbe una particella.
Si può allora viceversa congetturare che una particella, dotata di energia cinetica
e
quantità di moto p perpendicolare alle pareti, possa essere descritta da un sistema di infinite armoniche.
Accettando questa congettura, se il numero di armoniche non è infinito, l'ampiezza di Δx risulta > 0; c'è quindi una indeterminazione sulla posizione della particella, tanto maggiore quanto minore è il numero di armoniche.
animazione